In this brief post, we investigate the topological foundations of analysis. We limit the scope to the topology of a metric space. In particular, we provide the knowledge that is needed for the application to probability and measure theory.
A good introduction for all German-speakers is also provided by Prof. Dr. Edmund Weitz as embedded in the Appendix.
The objective of the next section is to prepare the very basic concept for the definition of a topological space. We start by defining an open and a closed ball, a neighborhood, interior point, an open and a closed set. All these definitions are interlinked to each other as we will see later on.
Parts of this post are based on [1] and [2].
Contents
Basic Definitions & Properties
Balls, Open & Closed Sets & Neighborhoods
Let ![]() denote a metric space.
denote a metric space.
Definition 1.1
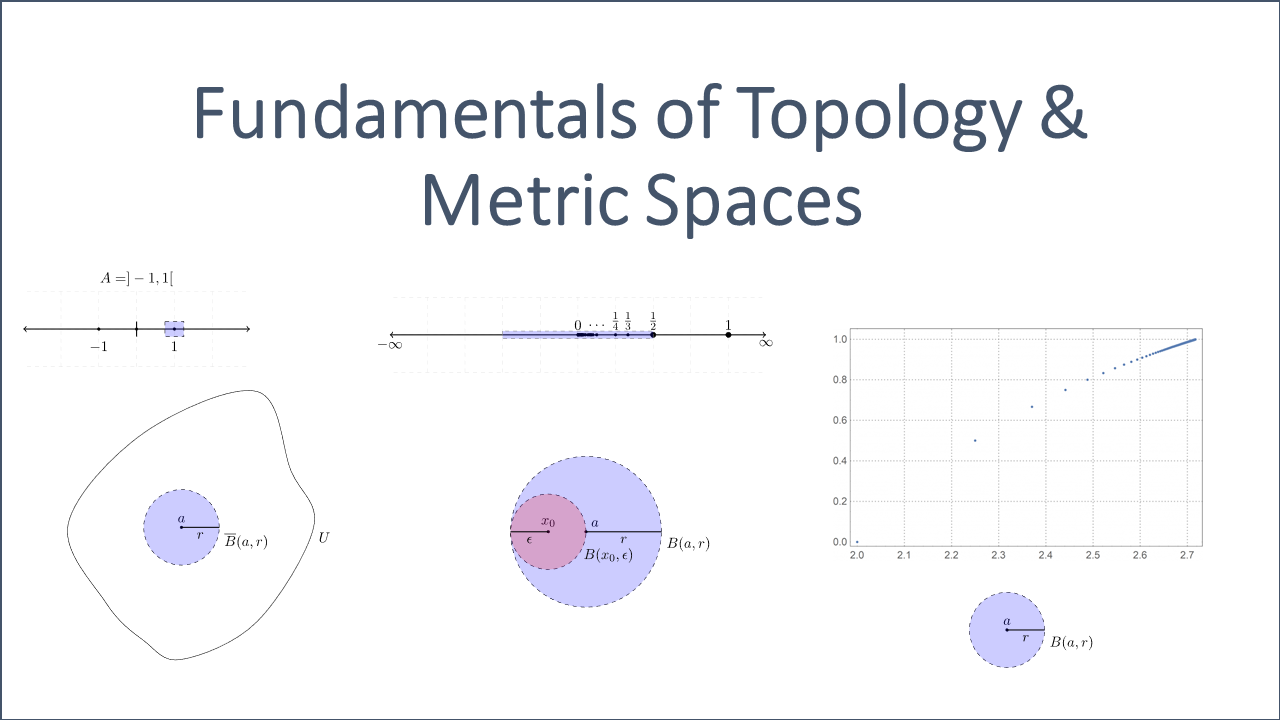
An (open) ball ![]() of radius
of radius ![]() and center
and center ![]() is the set of all points of distance less than
is the set of all points of distance less than ![]() from
from ![]() , i.e.
, i.e. ![]() .
.
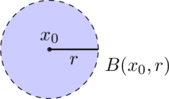
A closed ball ![]() of radius
of radius ![]() is the set of all points of distance less than or equal to
is the set of all points of distance less than or equal to ![]() from
from ![]() , i.e.
, i.e. ![]() .
.
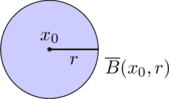
A subset ![]() of
of ![]() is called a neighborhood of
is called a neighborhood of ![]() if there is some
if there is some ![]() such that
such that ![]() .
.

An element ![]() is called an interior point of
is called an interior point of ![]() if there is a neighborhood
if there is a neighborhood ![]() of
of ![]() such that
such that ![]() .
.
A set ![]() of
of ![]() is called open if every point of
is called open if every point of ![]() is an interior point.
is an interior point.
![]()
The introduced concepts “interior point” and “open set” (and hence also the concept of “closed sets”) depend on the surrounding metric space ![]() . It is sometimes useful to make this explicit by saying “
. It is sometimes useful to make this explicit by saying “![]() is an interior point of
is an interior point of ![]() with respect to
with respect to ![]() ” or “
” or “![]() is open in
is open in ![]() “.
“.
By definition, every superset of a ball is considered to be a neighborhood. Neighborhoods can be defined without mentioning explicitly the corresponding metric space.
Example 1.1
An open ball in ![]() is an open interval
is an open interval ![]() . However, if we consider
. However, if we consider ![]() embedded in
embedded in ![]() , then
, then ![]() is apparently not an open ball in
is apparently not an open ball in ![]() .
.
For the sake of illustration we sketch a 2-dimensional open ball (i.e. an open interval) as a rectangle even though it would actually be a line without end-points. These end-points are illustrated by the lines crossing the x-axis.
The heuristic reasoning for that is that a one-dimensional interval cannot contain an open two-dimensional ball not matter how small the radius of this ball might be.
![]()
Apparently, ![]() is an interior point of
is an interior point of ![]() if and only if there is some real
if and only if there is some real ![]() such that
such that ![]() . In addition,
. In addition, ![]() is open if and only if
is open if and only if ![]() is a neighborhood of each of its points.
is a neighborhood of each of its points.
Example 1.2
Let us consider open and closed balls in ![]() along with the standard Euclidean metric
along with the standard Euclidean metric ![]() . Every open ball
. Every open ball ![]() ,
, ![]() in
in ![]() is an open set. Let
is an open set. Let ![]() be an arbitrary point. Set
be an arbitrary point. Set ![]() and consider
and consider ![]() with
with ![]() .
.
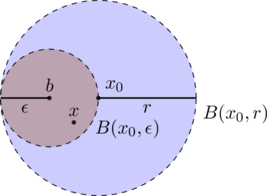
For all ![]() we have
we have
![]()
and so ![]() is contained in
is contained in ![]() . This shows that the arbitrary point
. This shows that the arbitrary point ![]() is an interior point of
is an interior point of ![]() and thus an open ball
and thus an open ball ![]() is an open set.
is an open set.
![]()
That is, a set ![]() is open if and only if for every
is open if and only if for every ![]() an open ball
an open ball ![]() exists such that
exists such that ![]() .
.
Definition 1.2 (Boundary Point)
Let ![]() and
and ![]() . Then,
. Then, ![]() is called boundary point for
is called boundary point for ![]() if
if
(1) 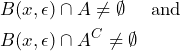
for all ![]() . The set of all boundary points is denoted by
. The set of all boundary points is denoted by ![]() .
.
![]()
Boundary points are just points on the boundary between the set ![]() and the surrounding basis set
and the surrounding basis set ![]() (i.e.
(i.e. ![]() of the metric space
of the metric space ![]() .
.

![]() can be contained in
can be contained in ![]() or in
or in ![]() . If all boundary points
. If all boundary points ![]() are outside of
are outside of ![]() , i.e. if
, i.e. if ![]() , then it is an open set.
, then it is an open set.
Definition 1.3 (Closed Set)
A set ![]() of
of ![]() is called closed in
is called closed in ![]() if its complement
if its complement ![]() is open in
is open in ![]() .
.
![]()
Equivalently, if all boundary points of ![]() are inside the set
are inside the set ![]() , i.e. if
, i.e. if ![]() , then it is a closed set. This also means that the set
, then it is a closed set. This also means that the set ![]() is always a closed set no matter what
is always a closed set no matter what ![]() is. The set
is. The set ![]() is then also called the closure of
is then also called the closure of ![]() .
.
Example 1.3
(a) The interval ![]() is closed in
is closed in ![]() .
.
Let ![]() denote a real number that is not an element of
denote a real number that is not an element of ![]() . Then,
. Then, ![]() and the ball
and the ball ![]() with
with ![]() has empty intersection with
has empty intersection with ![]() .
.
Hence, the complement ![]() is open and so the set
is open and so the set ![]() is closed.
is closed.

For the sake of illustration we sketch a 2-dimensional open ball as a rectangle even though it would actually be a line without end-points.
Note that all closed intervals in ![]() are of the form
are of the form ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
Let us now consider the set ![]() . For all
. For all ![]() and
and ![]() we have
we have ![]() . Hence, the set
. Hence, the set ![]() is open in
is open in ![]() .
.
Note that all open intervals in ![]() are of the form
are of the form ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
(b) Now consider the metric space ![]() with
with ![]() with the same distance function
with the same distance function ![]() ,
, ![]() as in (a).
as in (a).
The set ![]() is an open set since for all
is an open set since for all ![]() we consider the open ball
we consider the open ball ![]() with
with ![]() . That is, we determine the shortest distance between
. That is, we determine the shortest distance between ![]() and the two points
and the two points ![]() and
and ![]() and divide it by 2. Then, the corresponding open ball
and divide it by 2. Then, the corresponding open ball ![]() is contained within the set
is contained within the set ![]() . For the point
. For the point ![]() , we can consider the open ball
, we can consider the open ball ![]() with
with ![]() , for instance. This open ball equals
, for instance. This open ball equals ![]() since all the figures right from
since all the figures right from ![]() until 5 are not contained in
until 5 are not contained in ![]() . Hence,
. Hence, ![]() is open.
is open.
The set ![]() is also closed since
is also closed since ![]() is included in
is included in ![]() . Note that
. Note that ![]() is not a boundary point since it is not an element of the metric space
is not a boundary point since it is not an element of the metric space ![]() . The point
. The point ![]() is not a boundary point since for
is not a boundary point since for ![]() , for instance,
, for instance, ![]() holds true.
holds true.
(c) Let us consider the metric space ![]() of all integers together with the discrete metric
of all integers together with the discrete metric 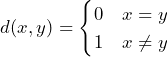 for all
for all ![]() . It follows that the open ball
. It follows that the open ball ![]()
![]() of radius
of radius ![]() and center at
and center at ![]() is either
is either ![]() if
if ![]() or
or ![]() if
if ![]() .
.
(d) Let us consider open and closed balls in ![]() along with the standard Euclidean metric
along with the standard Euclidean metric ![]() . Every closed ball
. Every closed ball ![]() ,
, ![]() in
in ![]() is a closed set. That is, we need to show that the complement set
is a closed set. That is, we need to show that the complement set ![]() is open. Let
is open. Let ![]() . Set
. Set ![]() and consider the open ball
and consider the open ball ![]() , that does not intersect with the closed ball
, that does not intersect with the closed ball ![]() due to the choice of
due to the choice of ![]() : Let
: Let ![]() , then the following holds due to the triangular property.
, then the following holds due to the triangular property.
![]()
and ![]() because of
because of ![]() .
.
Note that this also means that every isolated point in ![]() along with the Euclidean metric is a closed set.
along with the Euclidean metric is a closed set.
![]()
In the following section we are going to outline basic properties of open & closed sets, which will provide the heuristic for the definition of a topological space.
Properties of Open & Closed Sets
The following two propositions state basic properties of open and closed sets. It turns out that these properties characterize a topological space.
Proposition 1.1 (Open Sets)
Let ![]() be a family of open sets.
be a family of open sets.
(i) ![]() ;
;
(ii) ![]() if
if ![]() for an arbitrary index set
for an arbitrary index set ![]() ;
;
(iii) ![]() if
if ![]() for a finite index set
for a finite index set ![]() .
.
Proof:
(i) The empty set possesses every property since it does not have an element. Hence, the empty set is closed and open. Correspondingly, the set ![]() is open.
is open.
(ii) If ![]() then there must be an index
then there must be an index ![]() such that
such that ![]() with
with ![]() . All the more
. All the more ![]() holds true.
holds true.
(iii) Let ![]() with
with ![]() be open sets. Since
be open sets. Since ![]() there exists a
there exists a ![]() for each
for each ![]() with
with ![]() . If we set
. If we set ![]() then
then ![]() and the assertion follows.
and the assertion follows.
![]()
Why (iii) holds only true for finite index sets can also be seen if we try to prove that the intersection of two open balls at ![]() is open again. Just chose
is open again. Just chose ![]() for the open ball of the intersection
for the open ball of the intersection ![]() . This can be iterated provided that the index set is finite.
. This can be iterated provided that the index set is finite.
Please note that the proof above would also be valid if we use neighborhoods instead of balls. This would mean that the proof is not dependent on the used metric space and suggests that we could derive a new mathematical structure from it, where –in general– no algebraic operations, distance functions or orders need to be defined. However, given that we restrict our-self to topology for metric spaces, we will not further outline this idea.
The proof of the corresponding proposition for closed sets is apparent given the definition of a closed set.
Proposition 1.2 (Closed Sets)
Let ![]() be a family of closed sets.
be a family of closed sets.
(i) ![]() ;
;
(ii) ![]() if
if ![]() for an arbitrary index set
for an arbitrary index set ![]() ;
;
(iii) ![]() if
if ![]() for a finite index set
for a finite index set ![]() .
.
Proof:
Apply the definition and Proposition 1.1 (Open Sets).
![]()
Example 1.4
Let us continue Example 1.3. The intersection of a finite number of intervals ![]() is closed in
is closed in ![]() . Without loss of generality, let
. Without loss of generality, let ![]() . All the sets
. All the sets ![]() are closed and so is
are closed and so is ![]() in
in ![]() .
.
Let us now consider the family of open sets ![]() . For all elements
. For all elements ![]() of all open sets
of all open sets ![]() , we can find an open ball
, we can find an open ball ![]() . Hence, the union of these sets also contain open balls for all elements and is thus an open set itself.
. Hence, the union of these sets also contain open balls for all elements and is thus an open set itself.
![]()
Example 1.5
An infinite intersection of open sets need not to be open. Consider ![]() in
in ![]() . Apparently, there cannot be an
. Apparently, there cannot be an ![]() such that
such that ![]() .
.
Correspondingly, infinite unions of closed sets need not to be closed. To this end, consider ![]() in
in ![]() .
.
![]()
Accumulation and Limit Points
Closely related to closed sets are so-called accumulation and limit points. In addition, this section will pave the way to one of the below application of a topological space — limits.
Definition 1.2 (Accumulation & Limit Point)
Let ![]() and
and ![]() . We call
. We call ![]() an accumulation point of
an accumulation point of ![]() if every neighborhood of
if every neighborhood of ![]() in
in ![]() has non-empty intersection with
has non-empty intersection with ![]() .
.
The element ![]() is called limit point of
is called limit point of ![]() if every neighborhood of
if every neighborhood of ![]() in
in ![]() contains a point of
contains a point of ![]() other than
other than ![]() . Finally we set
. Finally we set
![]()
![]()
Every point within an open set but also every limit point of this set is an accumulation point as illustrated in the following example. Here, ![]() is the open interval in the standard metric space
is the open interval in the standard metric space ![]() .
.
Every point in ![]() is an interior, an accumulation and a limit point of
is an interior, an accumulation and a limit point of ![]() . Note that an interior point of
. Note that an interior point of ![]() requires to have a neighborhood
requires to have a neighborhood ![]() that is contained in
that is contained in ![]() . Given that
. Given that ![]() is an open set this holds true for all points within the set
is an open set this holds true for all points within the set ![]() by definition.
by definition.
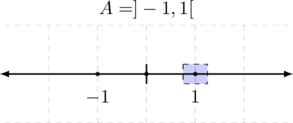
The ‘boundary’ points ![]() and
and ![]() are no interior points but limit and accumulation points of
are no interior points but limit and accumulation points of ![]() . Why?
. Why?
Because we can define any open ball around it and the intersection with ![]() will always contain a point different from
will always contain a point different from ![]() .
.
Let us now consider a set ![]() with a single isolated point in the metric space
with a single isolated point in the metric space ![]() . Is
. Is ![]() , that is the only element of the set, an accumulation and/or a limit point of
, that is the only element of the set, an accumulation and/or a limit point of ![]() ?
?
Apparently, every neighborhood ![]() of
of ![]() in
in ![]() has non-empty intersection with
has non-empty intersection with ![]() , i.e.
, i.e. ![]() . However,
. However, ![]() is not a limit point since the intersection
is not a limit point since the intersection ![]() does not contain a point other than
does not contain a point other than ![]() .
.
According to our thoughts above, elements of ![]() are accumulation points of
are accumulation points of ![]() . This fact is also reflected in the next proposition.
. This fact is also reflected in the next proposition.
Proposition 1.3: Let ![]() be a subset of a metric space
be a subset of a metric space ![]() .
.
(i) ![]() ;
;
(ii) ![]() if and only if
if and only if ![]() is closed.
is closed.
Proof: (i) See argumentation above.
(ii) ‘![]() Let
Let ![]() . Since
. Since ![]() is not an accumulation point of
is not an accumulation point of ![]() , there is some
, there is some ![]() of all neighborhoods of
of all neighborhoods of ![]() such that
such that ![]() . Thus,
. Thus, ![]() , that is,
, that is, ![]() is an interior point of
is an interior point of ![]() . Consequently
. Consequently ![]() is open and
is open and ![]() is closed in
is closed in ![]() .
.
‘![]() Let
Let ![]() be closed in
be closed in ![]() . Then
. Then ![]() is open in
is open in ![]() according to its definition. For any
according to its definition. For any ![]() , there is some
, there is some ![]() such that
such that ![]() . This means that
. This means that ![]() and
and ![]() are disjoint, and so
are disjoint, and so ![]() is not an accumulation point of
is not an accumulation point of ![]() , i.e.,
, i.e., ![]() . Hence, we have proved the inclusion
. Hence, we have proved the inclusion ![]() , which is equivalent to
, which is equivalent to ![]() . With (i), this implies
. With (i), this implies ![]() .
.
![]()
The limit points of a set ![]() are the limits of certain sequences in
are the limits of certain sequences in ![]() .
.
Proposition 1.4: An element ![]() of
of ![]() is a limit point of
is a limit point of ![]() if and only if there is a sequence
if and only if there is a sequence ![]() in
in ![]() which converges to
which converges to ![]() .
.
Proof: Let ![]() be a limit point of
be a limit point of ![]() . For each
. For each ![]() , choose some element
, choose some element ![]() in
in ![]() . Then
. Then ![]() is a sequence in
is a sequence in ![]() such that
such that ![]() .
.
Conversely, let ![]() be a sequence in
be a sequence in ![]() such that
such that ![]() . Then, for each neighborhood
. Then, for each neighborhood ![]() of
of ![]() , there is some
, there is some ![]() such that
such that ![]() . This means that
. This means that ![]() . Hence, each neighborhood of
. Hence, each neighborhood of ![]() contains an element of
contains an element of ![]() other than
other than ![]() .
.
![]()
Corollary 1.1: An element ![]() is an accumulation point of
is an accumulation point of ![]() if and only if there is a sequence
if and only if there is a sequence ![]() in
in ![]() such that
such that ![]() .
.
Proof: If ![]() is a limit point, then the claim follows from Proposition 1.4. Otherwise, if
is a limit point, then the claim follows from Proposition 1.4. Otherwise, if ![]() is an accumulation point, but not a limit point of
is an accumulation point, but not a limit point of ![]() , then there is a neighborhood
, then there is a neighborhood ![]() of
of ![]() such that
such that ![]() . Thus,
. Thus, ![]() , and the constant sequence
, and the constant sequence ![]() with
with ![]() for all
for all ![]() has the desired property.
has the desired property.
![]()
We can also characterize closed sets using convergent sequences by simply using the fact that a closed set is the complement of an open set.
Proposition 1.5: For ![]() , the following are equivalent:
, the following are equivalent:
(i) ![]() is closed;
is closed;
(ii) ![]() contains all its limit points;
contains all its limit points;
(iii) Every sequence in ![]() , which converges in
, which converges in ![]() , has its limit in
, has its limit in ![]() .
.
Proof: ‘(i) ![]() (ii)’ Any limit point of
(ii)’ Any limit point of ![]() is also an accumulation point and so is contained in
is also an accumulation point and so is contained in ![]() . Since
. Since ![]() is closed and Proposition 1.3,
is closed and Proposition 1.3, ![]() , and so all limit points are in
, and so all limit points are in ![]() .
.
‘(ii) ![]() (iii)’ Let
(iii)’ Let ![]() be a sequence in
be a sequence in ![]() such that
such that ![]() in
in ![]() . Then, by Corollary 1.1,
. Then, by Corollary 1.1, ![]() is an accumulation point of
is an accumulation point of ![]() . This means that, either
. This means that, either ![]() is in
is in ![]() , or
, or ![]() is a limit point of
is a limit point of ![]() , so, by assumption,
, so, by assumption, ![]() .
.
‘(iii) ![]() (i)’ This implication follows from Proposition 1.3 and Corollary 1.1.
(i)’ This implication follows from Proposition 1.3 and Corollary 1.1.
![]()
Compact Sets
Compact sets are so important since they possess important properties, that are known from finite sets:
- Set is bounded;
- Set contains a maximal and minimal element;
- An infinite sequence contains a constant subsequence.
The famous Heine-Borel Theorem will show that compact sets in metric spaces do indeed have these properties. However, we will only partly prove this theorem but will provide links and references to full proofs.
The analogy is also outlined in this really nice video (in German only) by Prof. Dr. Edmund Weitz.
Let us start with very basic but important definitions.
Definition 1.3 ((Open) Cover and Open Sub-Cover)
By an open cover ![]() of a set
of a set ![]() in a metric space
in a metric space ![]() , we mean a collection
, we mean a collection ![]() of (open) subsets of
of (open) subsets of ![]() such that
such that ![]() .
.
A sub-collection ![]() with
with ![]() of an (open) cover is called an open sub-cover of
of an (open) cover is called an open sub-cover of ![]() .
.
![]()
An (open) cover of ![]() is a collection of possibly overlapping open sets in
is a collection of possibly overlapping open sets in ![]() which, after considering their union globally, contains the set
which, after considering their union globally, contains the set ![]() inside.
inside.
Example 1.6 (Real Line)
Let us consider the set ![]() of the metric space
of the metric space ![]() . Then,
. Then, ![]() is an open cover of
is an open cover of ![]() because
because ![]() . This cover apparently contains infinitely many open sets
. This cover apparently contains infinitely many open sets ![]() .
.
![]() is an open subcover of
is an open subcover of ![]() since
since ![]() but
but ![]() . This subcover, however, still contains infinitely many open sets.
. This subcover, however, still contains infinitely many open sets.
![]()
Now we have the ingredients for the central definition of this section.
Definition 1.3 (Compact Set)
A subset ![]() of a metric space
of a metric space ![]() is said to be compact if every open cover
is said to be compact if every open cover ![]() of
of ![]() contains a finite subcover.
contains a finite subcover.
![]()
The definition of a compact set contains a very powerful requirement: it requires the existence of a finite open subcover within any possibly infinite open cover. Please also refer to the analogy to the properties of finite sets as mentioned at the beginning of this section.
It is clear that every finite set is compact.
Example 1.7 (Finite Set & Compactness)
Let ![]() be a finite set in the metric space
be a finite set in the metric space ![]() and
and ![]() . Note that we could chose any
. Note that we could chose any ![]() for this purpose. Apparently,
for this purpose. Apparently, ![]() is a finite and open cover of
is a finite and open cover of ![]() .
.
Each point of the finite set ![]() is contained in some open set by the cover depending upon that point. This directly implies that there is a finite sub-cover most the size of the set
is contained in some open set by the cover depending upon that point. This directly implies that there is a finite sub-cover most the size of the set ![]() .
.
![]()
Let us generalize the approach taken in Example 1.7 for an arbitrary non-empty set ![]() . By setting
. By setting
![]()
with ![]() , an open set
, an open set ![]() is assigned to each point
is assigned to each point ![]() . Hence, the set
. Hence, the set ![]() is an open cover for any set
is an open cover for any set ![]() .
.
The Heine-Borel theorem states that every closed and bounded set in ![]() ,
, ![]() is compact. This theorem is very important for analysis, measure theory and beyond.
is compact. This theorem is very important for analysis, measure theory and beyond.
Theorem 1.1 (Heine-Borel)
Let ![]() be a subset of the standard Euclidean metric space
be a subset of the standard Euclidean metric space ![]() with
with ![]() . Then the following statements are eqivalent:
. Then the following statements are eqivalent:
(i) ![]() is compact;
is compact;
(ii) ![]() is closed and bounded;
is closed and bounded;
(iii) Every infinite subset of ![]() has an accumulation point in
has an accumulation point in ![]() .
.
Part of the Proof for ![]() :
:
First, we assume that ![]() is compact i.e. that every open cover admits a finite sub-cover. Define
is compact i.e. that every open cover admits a finite sub-cover. Define ![]() . Then
. Then ![]() simply because the index set is
simply because the index set is ![]() itself and
itself and ![]() with
with ![]() is a open cover and thus there exist a finite sub-cover
is a open cover and thus there exist a finite sub-cover ![]() ,
, ![]() ,
, ![]() ,
, ![]() with
with ![]() and
and ![]() . Note that
. Note that ![]() with
with ![]() . Since this interval is bounded so is
. Since this interval is bounded so is ![]() .
.
Now, let us assume that ![]() is not closed (i.e. complement is open). Then, there must be a limit point of
is not closed (i.e. complement is open). Then, there must be a limit point of ![]() with
with ![]() since a closed set contains all its limit points [according to Proposition 1.5]. Find
since a closed set contains all its limit points [according to Proposition 1.5]. Find ![]() such that
such that ![]() . Define
. Define ![]() . Apparently,
. Apparently, ![]() and thus because of the assumption that
and thus because of the assumption that ![]() is compact there must be a finite sub-cover
is compact there must be a finite sub-cover ![]() ,
, ![]() ,
, ![]() ,
, ![]() with
with ![]() and
and ![]() . Set
. Set ![]() and find a
and find a ![]() such that
such that ![]() (which is possible since
(which is possible since ![]() ). According to the definition of
). According to the definition of ![]() this implies
this implies ![]() , which is a contradiction. Hence,
, which is a contradiction. Hence, ![]() is closed.
is closed.
For a general proof of the theorem for ![]() please refer to Theorem 3.31 in [1] or see there. Also note that a visualization by the University of Hannover of one proof can be found on YouTube. There is also a proof analysis of one direction of the Heine-Borel Theorem.
please refer to Theorem 3.31 in [1] or see there. Also note that a visualization by the University of Hannover of one proof can be found on YouTube. There is also a proof analysis of one direction of the Heine-Borel Theorem.
![]()
Topological Spaces
Topological spaces can be defined in many ways, however, given our focus on metric spaces and open sets the following definition is the most natural one. Please note that we could also use the properties of closed sets to define a topological space.
Definition 2.1 (Topological Space)
A topological space is a pair ![]() , where
, where ![]() is a set and
is a set and ![]() is a family of subsets that satisfies
is a family of subsets that satisfies
(i) ![]() ;
;
(ii) ![]() if
if ![]() for an arbitrary index set
for an arbitrary index set ![]() ;
;
(iii) ![]() if
if ![]() for a finite index set
for a finite index set ![]() .
.
![]()
The following video provides a rather unorthodox way of thinking about a topology. However, it might help to get a heuristic for topological spaces. It also mentions the connection between metrics and a topology.
Example 2.1 (Topologies):
a) If ![]() is a metric space and
is a metric space and ![]() is the set of all open sets, then
is the set of all open sets, then ![]() is a topology according to Proposition 1.1.
is a topology according to Proposition 1.1.
b) Let ![]() be a set and
be a set and ![]() then
then ![]() is the so-called trivial or indiscrete topology.
is the so-called trivial or indiscrete topology.
c) The power set ![]() of a set
of a set ![]() is the so-called discrete topology. In this topology every subset it open.
is the so-called discrete topology. In this topology every subset it open.
![]()
Continuous Functions, Open and Closed Sets
Now, we connect two important concepts via the following theorem.
Theorem 3.3 (Continuous Functions & Closed/Open Sets):
Let ![]() be a function between metric spaces
be a function between metric spaces ![]() and
and ![]() . Then the following are equivalent:
. Then the following are equivalent:
(i) ![]() is continuous;
is continuous;
(ii) ![]() is open in
is open in ![]() for each open set
for each open set ![]() ;
;
(iii) ![]() is closed in
is closed in ![]() for each closed set
for each closed set ![]() .
.
Proof: ‘(i) ![]() (ii)’ Suppose
(ii)’ Suppose ![]() is continuous on
is continuous on ![]() and let
and let ![]() be an open set. If
be an open set. If ![]() , then the claim follows from Proposition 1.1 (i). Thus, we suppose that
, then the claim follows from Proposition 1.1 (i). Thus, we suppose that ![]() .
.
Let ![]() . Due to the fact that
. Due to the fact that ![]() is open, we can chose at least one
is open, we can chose at least one ![]() such that
such that ![]() for every
for every ![]() . Given that
. Given that ![]() is continuous on
is continuous on ![]() , a corresponding
, a corresponding ![]() exists such that
exists such that
![]()
and ![]() . That is,
. That is, ![]() implies
implies ![]() . Thus,
. Thus, ![]() , which means that
, which means that ![]() is an open set.
is an open set.
‘(ii) ![]() (i)’ Let us suppose that
(i)’ Let us suppose that ![]() is open whenever
is open whenever ![]() is open and we aim to prove that
is open and we aim to prove that ![]() is continuous at each point of
is continuous at each point of ![]() . Given
. Given ![]() and
and ![]() , we know that the ball
, we know that the ball ![]() is open in
is open in ![]() . By assumption so is
. By assumption so is ![]() . Since
. Since ![]() and
and ![]() is an open set, there must be a
is an open set, there must be a ![]() such that
such that ![]() . This proves the assertion.
. This proves the assertion.
![]()
Please also refer to some counterexamples illustrating that the image of an open (closed) set under a continuous function does not need to be open (closed).
Appendix
For all German-speakers, I recommend to listen to the following quite illustrative video about metric spaces and topologies.
In addition, the next video introduces open and closed sets in an illustrative manner.
Literature:
[1]
[2]