Contents
Introduction
The assumption of independent and identically distributed random variables, short i.i.d., might be quite handy since it simplifies several statistical methods. The strong law of large numbers as well as the central limit theorem, for instance, assume independent variables. Benefiting from the independence while being able to incorporate dependency structures between random variables would therefore be very useful. And indeed, there is a way how to sneak in correlations in a given setting of i.i.d. random variables. One of those techniques are mixture models such as the binomial- and the Poisson-mixture model that are both studied in this post. The following is mainly based on [1].
Let ![]() be a suitable probability space and assume that we are interested in a set of
be a suitable probability space and assume that we are interested in a set of ![]() random variables
random variables ![]() .
.
Bernoulli-Mixture Model
A Bernoulli trial (or binomial trial) ![]() is a random experiment with exactly two possible outcomes which we can call “success” and “failure”. The “success” outcome, often represented by 1, appears with probability
is a random experiment with exactly two possible outcomes which we can call “success” and “failure”. The “success” outcome, often represented by 1, appears with probability ![]() , while the “failure” state, represented by 0, appears with complement probability
, while the “failure” state, represented by 0, appears with complement probability ![]() .
.
One of the simplest stochastic processes, the so-called Bernoulli process, is simply a set of Bernoulli trials.
Example 1:
Let us assume that ![]() represents the creditworthiness of counterparty
represents the creditworthiness of counterparty ![]() of a credit portfolio
of a credit portfolio ![]() . It is natural to model the two states “survival” and “default” by using a Bernoulli process with
. It is natural to model the two states “survival” and “default” by using a Bernoulli process with ![]() for all counterparties
for all counterparties ![]() . That is,
. That is, ![]() can take on the following two states:
can take on the following two states:
 with probability
with probability 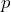 , if the counterparty goes bankrupt, and,
, if the counterparty goes bankrupt, and,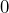 with probability
with probability 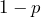 , if the counterparty survives.
, if the counterparty survives.
Here, ![]() is the probability of default of counterparty
is the probability of default of counterparty ![]() which is usually derived from a corresponding credit rating and suitable historical default rates.
which is usually derived from a corresponding credit rating and suitable historical default rates.
![]()
Another popular example of a Bernoulli trial/process is tossing a coin, where one side appears with probability ![]() .
.
More formally, a Bernoulli process ![]() is a (finite) sequence of independent random variables
is a (finite) sequence of independent random variables ![]() with
with
(1) 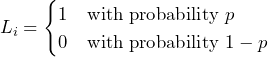
as Bernoulli trial with probability ![]() .
.
A Bernoulli process is therefore a sequence of independent identically distributed Bernoulli trials. Given the discrete nature of the Bernoulli trial, the expectation ![]() as well as the variance
as well as the variance ![]() for counterparty
for counterparty ![]() is given by
is given by
(2) ![Rendered by QuickLaTeX.com \begin{align*} \mathbb{E}(L_i) &= (1 \cdot p) + (0 \cdot (1-p)) = p \\ \mathbb{E}(L_i^2) &= (\mathbb{P}[L_i=1] \cdot 1^2) + (\mathbb{P}[L_i=0] \cdot 0^2) = p \\ \mathbb{V}(L_i) &= \mathbb{E}(L_i^2)- \mathbb{E}(L_i)^2 = p-p^2 = p(1-p). \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-13a0f2a68e006d357a5099feb38b5d42_l3.png)
In the next sections we will have a closer look at the Bernoulli process and we will relax the assumption of independence between them.
Sum of i.i.d. Bernoulli Random Variables with constant Parameter
For the sake of illustration let us assume that all random variables are mutually independent and that all random variables do have the same probability ![]() assigned. That is,
assigned. That is, ![]() is a Bernoulli process with probability
is a Bernoulli process with probability ![]() . In this case the distribution of the sum
. In this case the distribution of the sum
(3) 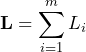
is governed by the binomial distribution ![]() .
.
Example 2:
We continue Example 1 and consider the sum ![]() of the corresponding Bernoulli process
of the corresponding Bernoulli process ![]() that is distributed according to
that is distributed according to ![]() . The probability that
. The probability that ![]() out of
out of ![]() counterparties are going to default (“success”) is
counterparties are going to default (“success”) is ![]() .
.
For instance, if ![]() and
and ![]() then two defaults will occur with probability
then two defaults will occur with probability ![]() .
.
![]()
As illustrated, it is easy to calculate any feature of the distribution of ![]() . For instance, the expectation, the variance as well as the probability of a specific value
. For instance, the expectation, the variance as well as the probability of a specific value ![]() is given by:
is given by:
(4) ![Rendered by QuickLaTeX.com \begin{align*} \mathbb{E}(\mathbf{L}) &=m\cdot p \\ \mathbb{V}(\mathbf{L}) &=m\cdot p \cdot (1-p) \\ \mathbb{P}[\mathbf{L}=k] &= \binom{m}{k} p^k(1-p)^{m-k} \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-a8b40ba385685fbdcf96defa785d4f74_l3.png)
Beside that, it would also be quite simple to determine ![]() as well as the variance
as well as the variance ![]() by just knowing (2) and applying the additivity of the expectation and variance.
by just knowing (2) and applying the additivity of the expectation and variance.
In the next step we are going to incorporate correlation between the variables ![]() by using the distribution parameters
by using the distribution parameters ![]() . Notice that
. Notice that ![]() is a probability.
is a probability.
Sum of Independent Bernoulli Random Variables with Random Parameter
By treating the distribution parameters ![]() of the outlined Bernoulli process as random variables
of the outlined Bernoulli process as random variables ![]() , it is possible to incorporate a correlation. That is, we assume that
, it is possible to incorporate a correlation. That is, we assume that ![]() follows a joint distribution represented by the distribution function
follows a joint distribution represented by the distribution function ![]() with support in
with support in ![]() . Correspondingly, we assume
. Correspondingly, we assume ![]() , where
, where ![]() itself is considered to be a random variable.
itself is considered to be a random variable.
This kills two birds with one stone. First, we drop the assumption that all Bernoulli trials do have the same probability ![]() applied. Second, we can incorporate a correlation between the
applied. Second, we can incorporate a correlation between the ![]() random variables since the correlation
random variables since the correlation ![]() only depends on
only depends on ![]() and
and ![]() .
.
In more mathematical terms, let
(5) ![]()
Conditional on the realization of the parameters ![]() , the random variables
, the random variables ![]() are still independent. One could, for instance, assume that
are still independent. One could, for instance, assume that ![]() is uniformly distributed on
is uniformly distributed on ![]() as in the
as in the R code example below.
The joint distribution of ![]() is given by
is given by
(6) ![Rendered by QuickLaTeX.com \begin{align*} \mathbb{P}[L_1=l_1, \ldots, L_m=l_m] = \int_{[0,1]^m}{\prod_{i=1}^m{p_i^{l_i}(1-p_i)^{1-l_i}} \ dF(p_1, \ldots, p_m)} \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-eec25dabf62cb62f5b14a74f34747ff0_l3.png)
where ![]() {“failure”, “success”}. The representation (6) is possible since we can leverage on the independence.
{“failure”, “success”}. The representation (6) is possible since we can leverage on the independence.
The covariance between the marginal random variables equals
(7) ![]()
and therefore the correlation can be determined by
(8) ![]()
That is, the correlation between the two variables ![]() and
and ![]() is fully determined by the variables
is fully determined by the variables ![]() and
and ![]() . We can therefore use this backdoor to sneak in correlation using conditional independence.
. We can therefore use this backdoor to sneak in correlation using conditional independence.
The binomial-mixture model is analytically. Nonetheless, we can simulate both sides of the equations to double-check it by example. The following R code is one way to do so.
# Binomial Mixture Model:
# ---------
# Produce dependent uniform distributed variables by starting with multi-variate
# normal variables. We therefore need the following package
library(mvtnorm)
m <- 20 #nbr of variables
simulation.nbr <- 1000000 #nbr of simulations
# get correlated normal random variables
sigma <- diag(1, nrow = m, ncol = m)
# variable 2 and 3 shall be correlated with 0.5
sigma[2,3] <- 0.5
sigma[3,2] <- 0.5
# variable 12 and 20 shall be correlated with 0.8
sigma[12,20] <- 0.8
sigma[20,12] <- 0.8
# simulate the m-dimensional joint normal distribution
X <- rmvnorm(n=simulation.nbr, mean = rep(0,m), sigma = sigma)
# transform data into correlated prob on [0,1]^m
P <- pnorm(X)
# prepare data structure for variables
L <- matrix(nrow = simulation.nbr, ncol=m)
# simulate the Bernoulli distribution for each variable i
for(i in 1:m){
L[,i] <- ifelse(runif(simulation.nbr) < P[,i], 0, 1)
}
# By construction the following covariances should be in the same order
cov(P[,2],P[,3])
cov(L[,2],L[,3])
cov(P[,12],P[,20])
cov(L[,12],L[,20])
# By construction the following correlations should be in the same order
cov(P[,2],P[,3])/( sqrt(mean(P[,2])*(1-mean(P[,2]))) * sqrt(mean(P[,3])*(1-mean(P[,3]))))
cor(L[,2],L[,3])
cov(P[,12],P[,20])/( sqrt(mean(P[,12])*(1-mean(P[,12]))) * sqrt(mean(P[,20])*(1-mean(P[,20]))))
cor(L[,12],L[,20])
Please notice that we simulate a suitable Bernoulli process using the code ifelse(runif(simulation.nbr) < P[,i], 0, 1), where P[,i] carries the correlation information of the parameter ![]() already in it.
already in it.
Poisson-Mixture Model
A similar pattern is also used for Poisson-distributed random variables. Let us therefore assume that our random variables ![]() are distributed according to the Poisson distribution with intensity parameter
are distributed according to the Poisson distribution with intensity parameter ![]() , denoted by
, denoted by ![]()
![]()
![]() . The expectation as well as the variance of a Poisson-distributed random variable
. The expectation as well as the variance of a Poisson-distributed random variable ![]() is given by its intensity parameter, i.e.,
is given by its intensity parameter, i.e.,
(9) ![]()
The distribution of the sum of independent Poisson-distributed variables ![]() is determined by
is determined by
(10) 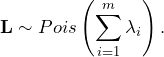
Given that we know the distribution of ![]() , it is easy to derive any feature such as expectation and variance:
, it is easy to derive any feature such as expectation and variance:
(11) 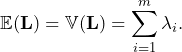
Just as in the binomial case we introduce correlation between the variables ![]() and
and ![]() with
with ![]() by assuming that
by assuming that ![]() is a random vector with distribution function
is a random vector with distribution function ![]() and support in
and support in ![]() .
.
Further we assume that conditionally on a realization ![]() of
of ![]() the variables
the variables ![]() with
with ![]() are independent:
are independent:
(12) ![]()
The joint distribution of ![]() is given by
is given by
(13) ![Rendered by QuickLaTeX.com \begin{align*} \mathbb{P}[L_1=l_1, \ldots, L_m=l_m] = \int_{[0,\infty]^m}{\prod_{i=1}^m{ \frac{\lambda_i^{l_i}}{l_i!} } \ dF(\lambda_1, \ldots, \lambda_m)} \end{align*}](https://www.deep-mind.org/wp-content/ql-cache/quicklatex.com-b56128ae548b5adf9dd7ffefa75b76a2_l3.png)
where ![]() .
.
The covariance between the marginal random variables equals
(14) ![]()
and therefore the correlation can be determined by
(15) ![]()
That is, the correlation between the two variables ![]() and
and ![]() is fully determined by the variables
is fully determined by the variables ![]() and
and ![]() . We can therefore use this backdoor to sneak the correlation in using conditional independence.
. We can therefore use this backdoor to sneak the correlation in using conditional independence.
The Poisson-mixture model is analytically. Nonetheless, we simulate both sides of the equations to double-check it by example. The following R code is one way to do so.
# Poisson Mixture Model:
# ---------
# Produce dependent variables on positive reals using multivariate discrete
# random variables and a Gaussian copula. To this end we use the GenOrd package:
library(GenOrd)
m <- 20 #nbr of variables
simulation.nbr <- 1000000
# since we want to have correlated random variables we need a corr matrix
sigma <- diag(1, nrow = m, ncol = m)
# variable 2 and 3 shall be correlated with 0.2
sigma[2,3] <- 0.2
sigma[3,2] <- 0.2
# variable 12 and 20 shall be correlated with 0.7
sigma[12,20] <- 0.7
sigma[20,12] <- 0.7
# to make it reproduceable
set.seed(1)
# list of m vectors representing the cumulative probabilities defining
# the marginal distribution of the i-th marginal distribution via the CDF
# that are all the same in our simple example
marginal.CDF <- rep(list(bquote()), m)
for(i in 1:m){
marginal.CDF[[i]] <- c(0.1, 0.3, 0.5, 0.6, 0.75)
}
# checks the lower and upper bounds of the correlation coefficients.
# in our case the two correlations lie within the thresholds
corrcheck(marginal.CDF)
# create correlated sample with given marginals
Lambda <- ordsample(n = simulation.nbr, marginal = marginal.CDF, Sigma = sigma)
# prepare data structure for the Poisson-distributed variables
# using the realized lambdas from variable Lambda
L <- array(0,dim=c(simulation.nbr*10, m))
# simulate the Poisson distribution for each variable i
for(i in 1:m){ # do for all variables L.i
L[,i] <- rpois(n = simulation.nbr*10, lambda = Lambda[,i])
}
# By construction the following covariances should be in the same order
cov(Lambda[,2],Lambda[,3])
cov(L[,2],L[,3])
cov(Lambda[,12],Lambda[,20])
cov(L[,12],L[,20])
# By construction the following correlations should be in the same order
cov(Lambda[,2],Lambda[,3])/( sqrt(var(Lambda[,2])+ mean(Lambda[,2])) * sqrt(var(Lambda[,3])+ mean(Lambda[,3])) )
cor(L[,2],L[,3])
cov(Lambda[,12],Lambda[,20])/( sqrt(var(Lambda[,12])+ mean(Lambda[,12])) * sqrt(var(Lambda[,20])+ mean(Lambda[,20])) )
cor(L[,12],L[,20])
Please notice that rpois(n=20, lambda=c(1,500)), for instance, generates a random variate using the two different intensity parameter ![]() and
and ![]() sharing the sample space of size
sharing the sample space of size ![]() . We therefore multiply the variable
. We therefore multiply the variable simulation.nbr by 10 to increase the quality of the approximation.
Literature:
[1]

