Introduction
In order to develop a useful theory of events with ‘uncertain’ outcome, it seems to be reasonable to give a clear, unambiguous interpretation of probability. This post is about two different types of interpretations of probability and thus not only relevant to mathematicians but also to philosophers and practitioners.
This post is mainly based on Walley [1], but also the other referenced literature is used. The section about uncertainty is mainly based on Decision Problems, Risk and Uncertainty as well as on [5] and the references therein.
Several videos and other articles are directly referenced within the post. It is recommended to check at least some of this embedded content since it will provide you with valuable background and in-depth information.
A very important aspect of such an interpretation is the inevitable uncertainty as outlined in Decision Problems, Risk and Uncertainty as well as in Uncertainty and Capacities in Finance. We are going to outline this topic in the corresponding context as well.
The idea of probability leads in two different directions: belief and frequency. Probability makes us think of the degree to which we can be confident of something uncertain, given what we know or can find out. Probability also makes us think of the relative frequency with which some outcome occurs on repeated trials on a chance setup.
Chapter 11 of [4], Ian Hacking.
The following two sections will outline the meaning of Aleatory (e.g. frequency) and Epistemic (e.g. belief) probability. Afterwards, we will explore the different applications in machine learning, politics and finance.
Aleatory Probability
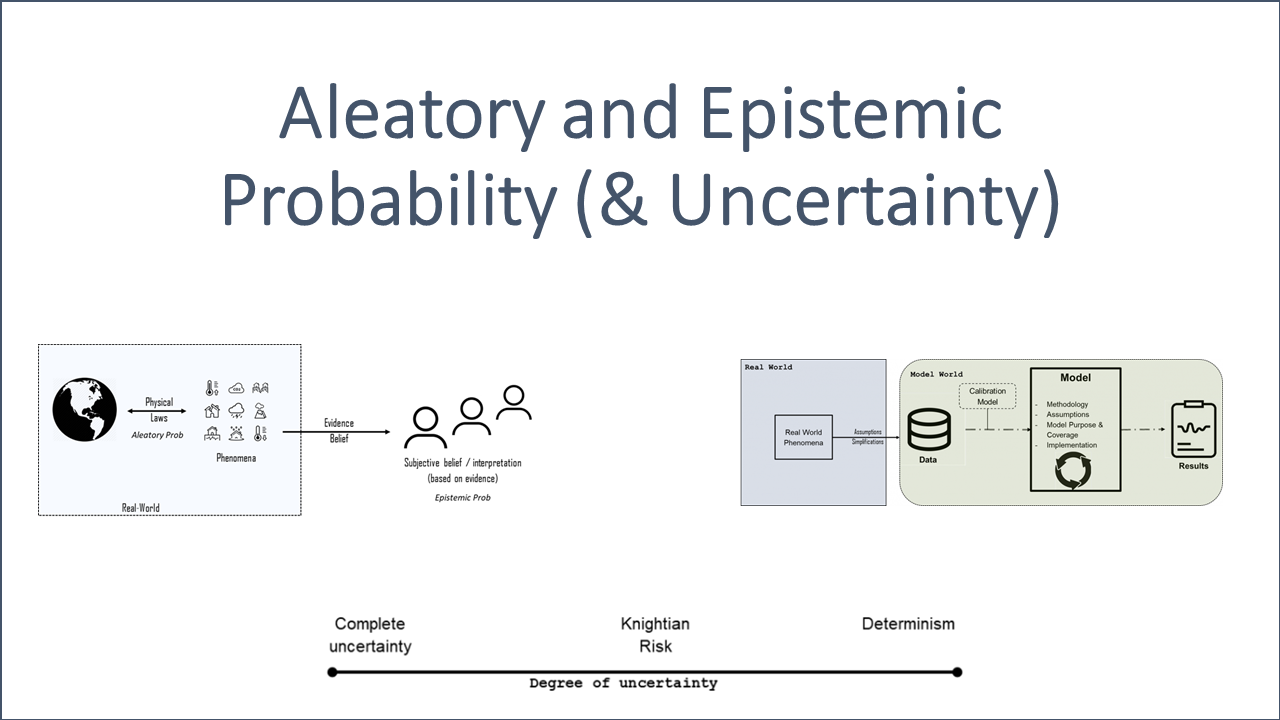
Aleatory, from alea, a Latin word for games of chance, is referring to the properties of real-world phenomena. Aleatory probabilities belong to a phenomena realizing via an event and are therefore independent from a subjective interpretation. These probabilities can be observed objectively and are therefore considered to be objective as illustrated in Fig. 1.
The probabilities involved in statistical models and scientific theories, which are intended to model randomness in the real-world, are examples of aleatory probabilities.
Let us study standard examples of probability theory in this context.
Example 2.1 (Games and Objective Probabilities)
Gambling games can be modeled with a well-defined experiment since the scope and its conditions are stable. In addition, the outcome of one game (e.g. rolling dices) does usually not affect other games, i.e., they are usually independent. Games can usually be repeated arbitrarily often and they can easily be simulated. If the games are conducted properly, the interpretation of the outcomes of many games should be objective to a certain degree. Gambling games follow the laws of physics and can therefore be interpreted as an aleatory probability.
![]()
One of the simplest gambling games is tossing a coin. Let us think about whether such a game can really be considered as random.
Coin tossing is definitely a physical phenomena that is based on the laws of classical mechanics but subject to chaos. That is, a small change in the initial conditions of the coin toss can lead to a totally different outcome. The outcome is, however, deterministic as outlined in the following videos.
Also note that machine learning can be used to also predict other chaotic systems as explained in Machine Learning’s ‘Amazing’ Ability to Predict Chaos.
Due to the fact that this is an incredibly hard problem, scientists usually simplify and treat these games as a random or stochastic process. This approach is in general totally fine. Also refer to “Is it practical and useful to distinguish aleatoric and epistemic uncertainty?“.
Another video titled “The Search of Randomness” with Persi Diaconis outlines the deterministic property of tossing a coin even in more detail.
Aleatory probabilities appear not only in physics, but also in biological, economic, finance and psychological theories. These theories refer to empirical phenomena (such as flipping a coin), not to the beliefs of any person or group of persons.
There are two basic types of aleatory interpretation, each having several versions.
Frequentists interpretations identify probabilities with a property of (infinite) sequence of events. This interpretation regards probabilities as properties of classes and sequences of trials and it relies on observation and statistical data.
Propensity interpretations take the probability of a single event (not a sequence of events) to measure its tendency to occur in a particular kind of experiment. This interpretation regards probabilities as dispositional properties of real-world phenomena (e.g. physical symmetry of a fair coin). Propensity interpretation is theoretical and allow chances to be constructed from other physical properties through known laws, although typically the required laws are unknown and the chances must be inferred from statistical data.
(also referring to Hacking [4])
Processes that are really random, i.e. a process determined by nothing, cannot be predicted since there is no pattern or algorithm that is recognizable. Hence, more information would not help to increase the trust in any prediction. In 2022, many scientists guess that quantum mechanics is truly random. Check out the following nice video What is Random by Vsauce and Veritasium.
The following video further tries to capture the meaning of randomness and connects it with information theory.
In the next section, we are going to outline what an Epistemic probability is.
Epistemic Probability
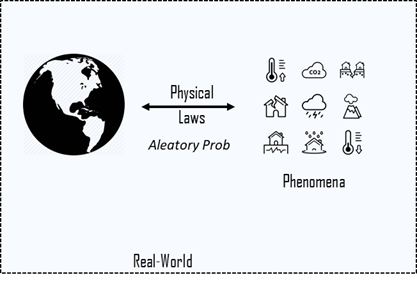
Epistemic probabilities model logical or psychological degrees of partial belief, of a person, agent or intentional system. Epistemic probabilities (unlike aleatory ones) depend on the available evidence and is subject to interpretation.
In particular, Epistemic probability is an interpretation of a real-world phenomena based on evidence.
The illustration in Fig. 2 shows the basic idea of Epistemic interpretations of probability. It is based on an interpretation and some sort of body of evidence. The more evidence we can use, the better the induction will be.
Example 3.1 (Games and Subjective Probabilities)
An alternative approach to Example 2.1 is to interpret the probability of a game as subjective beliefs. That is, a probability does not describe a property of an event but rather the subjective beliefs about it. The following quote from [1] underpins that distinction quite well:
‘This thumbtack has chance of 0.4 of landing pin-up’ is a statement of aleatory probability, because ‘chance’ denotes a physical property that does not depend on the observer. ‘He believes that the thumbtack will probably land pin-up’ is a statement of epistemic probability, because it refers to the beliefs of a specific observer. – P. Walley, [1].
![]()
Bayesian interpretation of probability is a special and very important case of Epistemic probability.
We can further distinguish the following types of Epistemic probability interpretation.
Logical interpretations, in which the epistemic probability of a hypothesis relative to a given body of evidence is uniquely determined.
Personalist interpretations, in which probabilities are constrained only by axioms of coherence and not by evidence. Probabilities should be constrained by the available evidence, but we do not yet have algorithms for determining unique (logical) probabilities from evidence.
Rationalistic interpretations, intermediate between the logical and personalist extremes, which require probabilities to be consistent in certain ways with the evidence, without requiring they be uniquely determined. By developing a rationalistic interpretation, we can move away from a personalist interpretation to a more logical one.
Aleatory and Epistemic Uncertainty
The general term uncertainty covers many aspects. Unknown states of natures, unknown probabilities, preferences of the decision maker, and many other things that are not yet known (i.e. unknown unknowns).
F. H. Knight first distinguished in 1921 between ‘risk’ and ‘uncertainty’ in his seminal book [3]. On the one hand, Knightian or complete uncertainty may be characterized as the complete absence of information or knowledge about a situation or an outcome of an event. Knightian risk, on the other hand, may be characterized as a situation, where the true information on the probability distribution is available. In practice, no parameter or distribution can be known for sure a priori. Hence, we find it preferable to think about degrees of uncertainty.

Coming back to gambling – discrete probability theory and combinatorics were conceived in the 16th and 17th century by mathematicians attempting to solve gambling problems (see [4]).
Due to the fact that conditions of gambling games are well-known and stable, the degree of uncertainty is comparatively low. Good (but not prefect) estimates of the corresponding (objective) probability distributions are known. In such cases, classical probability theory and/or the classical measure theory are the right tools to tackle these types of problems. Note that even games of chance are subject to a certain degree of uncertainty.
Aleatory uncertainty is also known as statistical uncertainty. This kind of uncertainty is reflected and incorporated in the data and thus it is also known as data uncertainty. This type of uncertainty cannot be reduced by the accumulation of more data and/or additional information. Hence, Aleatory uncertainty cannot be illustrated using Fig. 3 since additional information does not have an effect on its degree.
Example 4.1 (True Randomness)
Let us assume we have data at hand representing an event but we do not know whether this data represents a random process. It is a very hard problem to determine whether we deal with a random process or not since even a truly random process can generate patterns by coincidence. However, these patterns cannot be used to predict the future behavior of the process since a truly random process is determined by nothing. This also implies that you need to have a ‘long’ time series to have at least a chance to judge reasonably about its randomness. It also means that discovering patterns in the given time series does not necessarily mean that it is (not) a random process. Due to the fact that figuring out whether a process is random or not can be (in theory) be solved using a very, very long time series, it is more of an Epistemic-type.
Ultimately, there are only two possibilities: either the process is or is not random. Hence, the Aleatory uncertainty is actually only about this question.
![]()
Epistemic uncertainty, also known as systematic uncertainty, is attributable to the incomplete knowledge about a real-world phenomenon that affects the ability of the agent to model it. This may be because a measurement is not accurate, because the model neglects certain effects, or because particular data have been deliberately hidden, etc. and is therefore also called model uncertainty. This type of uncertainty can be reduced by increasing data since –at least in principle– we could know it better. Hence, additional data can push you further to the right in Fig. 3. This is ultimately the goal when conduction a model validation, increasing your data basis or improving your modeling approach in general.
Be aware of the different meaning of data and information. Data is what you need to generate information. For instance, you might need a long time series of some physical event to derive from that a small formula. This formula represents the amount of information that you have generated from it. This example might make it clear why the amount of information decreases when you move to the right of Fig. 3. If something is determined beforehand, there need to be some sort of algorithm to determine what is going to happen. Otherwise, there is not usable beforehand and no discoverable cause since it is truly random. If you want to pass on information from a truly random process you need to pass on all of the information since you cannot compress it using an algorithm.
Application in Machine Learning
Machine learning is about recognizing patterns in data using function approximation algorithms such as neural nets and regression. Also refer to the universal approximation theorem, which states that neural nets can approximate any ‘relevant’ function. Also refer to this article about an illustration of the corresponding proof.
These function approximation algorithms are used to extract a specific model from data. Learning in the sense of generalizing beyond the sample data seen so far is necessarily based on a process of induction.
Specific observations (sample data) are replaced by general patterns, which could also be considered as background models that generate data.
Approximation models can usually never be provably (i.e. deductively) correct but only hypothetical and therefore uncertain, and the same holds true for the classification or prediction generated by the model.
In addition to the uncertainty inherent in inductive inference, other sources of uncertainty exist, including incorrect model assumptions and noisy or imprecise data.
Relevant data usually reflect a real-world (random) phenomena and is therefore of aleatory nature. For instance, the time series of flipping a coin experiment reflects the seemingly random process that is governed by the laws of physics.
The following two videos roughly explain the backdrop and illustrate the application in machine learning.
Application in Politics
Let us consider a statement by Donald Rumsfeld, the former United States Secretary of Defense, in 2002.
Reports that say that something hasn’t happened are always interesting to me, because as we know, there are known knowns; there are things we know we know. We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns—the ones we don’t know we don’t know. And if one looks throughout the history of our country and other free countries, it is the latter category that tends to be the difficult ones.
– Donald Rumsfeld.
This statement is based on evidence and it applies rational arguments and an awareness of the inevitable uncertainty. Hence, it is clearly of Epistemic nature, which is typical in areas such as politics.
D. Rumsfeld applied a simple categorization in two dimensions:
- Awareness of the phenomenon (e.g. of the existence of a problem)
- Ignorance of the phenomenon (e.g. it’s existence is known, but it’s ignored anyway)
The following matrix comprises these combinations, whereas the first dimension refers to the degree of knowledge of an individual (knowledge vs. ignorance) while the second dimension refers to this individual degree of awareness (awareness of phenomenon vs. existence is not known).
| Knowledge (knowns) | Lack of Knowledge (unknowns) | |
| Awareness (known) | known knowns | known unknowns |
| Ignorance (unknown) | unknown knowns | unknown unknowns |
For instance, it might be the case that a group of people don’t know a certain fact. This group of people, however, can be split into two sub-groups:
- People who don’t know that they don’t know (unknown unknowns, i.e. ignorance)
- People who know that they don’t know (known unknowns)
Usually, category 1. is the more problematic as stated by D. Rumsfeld. The simple reason for that believe might be, that the degree of uncertainty is the highest in this category. We are not aware that we don’t know something of relevance.
Uncertainty and thus probability can also be categorized. The most fundamental distinction is between aleatory and epistemic concepts of probability.
Application in Finance
Even though there are strong arguments why it is useful not only to restrict to classical probability theory, it is still common in finance to apply exactly this type of model.
Example 7.1 (EuroStoxx 50)
Let us assume that we would like to project the development of EuroStoxx 50. A quite common way to model such a projection is to conduct a statistical analysis based on the time series of the EuroStoxx 50.
![]()
As outlined in Decision Problems, Risk and Uncertainty, it is actually ignorant to just focus on the corresponding time series of the EuroStoxx 50. Relevant real-world phenomena such as political changes or (financial) crisis usually affect the performance of stock indices significantly.
There is a high level of uncertainty since we might suspect but we do not know when the next crisis is coming up (known unknowns). In addition, we might miss a relevant event or fact completely (unkonwn unknowns). Quite often market practitioners simply ignore apparently wrong assumptions such as the normal distribution assumption (known unknowns).
Nonetheless, we need to make assumptions and simplifications in order to abstract from real world since it is far too complicated to be fully modeled.
![]()
Literature
Apart from the typical list of used literature, I would like to recommend the following YouTube video series about the interpretation of probability.
[1]
[2]
[3]
[4]
[5]
[6]