Introduction
There are many textbooks, posts, videos and papers about continuity. However, it is hard to find a cohesive introduction to the concept of continuity aimed at what is needed for the basics of measure and probability theory. The textbook by R. M. Dudley [2], however, is a fundamental introduction, which we recommend for experienced users to this end.
This blog post strives to provide an overview and an easy-to-read introduction to continuity for probability and measure theory by focusing on the motivation behind the definitions and statements. Many examples will illustrate the discussed objects and their logical relationships.
Understanding continuity at a point requires a profound knowledge about Inner Products, Norms and Metrics (i.e. distance functions) since continuity is about ‘small’ changes of function arguments relative to small changes of its (function) values. Distance functions combined with limits (and its underlying topology) of functions provide a measure to determine how ‘small’ might be interpreted.
Required Knowledge:
- Basic Analysis knowledge;
- Limits & Topological Spaces;
- Metric Spaces & Vector Spaces.
We restrict our considerations to the Euclidean metric space ![]() with the standard metric
with the standard metric ![]() . Please refer to Inner Products, Norms and Metrics for further details.
. Please refer to Inner Products, Norms and Metrics for further details.
Before we actually start, let us think about what we want to achieve with continuous functions. Why is this type of functions so important, not only from a pure theoretical but also from a very practical perspective?
The following heuristic tries to explain that in simple terms. Afterwards, we will start to introduce it formally.
A function behaves as continuous at ![]() if a small change in
if a small change in ![]() can be reached by a sufficiently small change in the corresponding argument
can be reached by a sufficiently small change in the corresponding argument ![]() .
.
Driving a car by operating the steering wheel might serve as a heuristic example of a continuous function ![]() . Consider the rotation of the steering wheel as the domain
. Consider the rotation of the steering wheel as the domain ![]() of the function
of the function ![]() that translates these input variables into the change in direction
that translates these input variables into the change in direction ![]() of the vehicle. You would like that the function
of the vehicle. You would like that the function ![]() is continuous since a small change in direction should be reached by a small change in the rotation angle of the steering wheel.
is continuous since a small change in direction should be reached by a small change in the rotation angle of the steering wheel.
Ultimately, continuity is all about controlled behavior of the function values relative to its elements of the domain. Even though this might not be a mathematical precise definition of continuity, it might help to understand and remind the actual definition of continuous functions better.
Be aware that we would like to control the behavior of the range since this is by design the area that should behave in a continuous manner.
Keep the following points in your mind:
- Continuity is all about controlled behavior of the function values;
- Different types of continuity basically just require different types of controlled behavior. For instance, one can ask for a controlled behavior at a specific point in the domain or for the entire function;
- Convergent (and Cauchy) sequences are closely interlinked with continuity. Refer to Limits & Topological Spaces for further details;
In the following, we consider the concept of continuity in 1-dimensional metric spaces. This will serve as the basis for the second part of this series, where we will also consider multi-dimensional metric spaces. Nonetheless, we are going to introduce the different concepts in a general way, such that it can be used in one and multi-dimensional metric spaces.
Let us start with the simplest form of continuity.
Continuity at a Point
Keep the heuristic –outlined above– in mind when reading the following definition.
Definition 2. 1(Continuous at a Point):
Let ![]() and
and ![]() be metric spaces and let
be metric spaces and let ![]() be a function from
be a function from ![]() to
to ![]() . The function
. The function ![]() is said to be continuous at a point
is said to be continuous at a point ![]() in
in ![]() if for every
if for every ![]() there is a
there is a ![]() , such that
, such that
(1) ![]()
If ![]() is continuous at every point of a subset
is continuous at every point of a subset ![]() of
of ![]() , we say
, we say ![]() is continuous on
is continuous on ![]() . If
. If ![]() is continuous on its domain, we say that
is continuous on its domain, we say that ![]() is continuous.
is continuous.
If ![]() is a point in the domain
is a point in the domain ![]() of the function
of the function ![]() , where
, where ![]() is not continuous, we say that
is not continuous, we say that ![]() is discontinuous at
is discontinuous at ![]() , or that
, or that ![]() has a discontinuity at
has a discontinuity at ![]() .
.
![]()
Definition 2.1 reflects the idea that points close to ![]() are mapped by
are mapped by ![]() to points sufficiently close to
to points sufficiently close to ![]() . That is,
. That is, ![]() behaves in a controlled manner. Keeping this heuristic in mind it is also clear why the formulation “for all
behaves in a controlled manner. Keeping this heuristic in mind it is also clear why the formulation “for all ![]() ” makes sense — if the function
” makes sense — if the function ![]() should behave in a controlled manner the corresponding range of the function needs to behave controlled in relation to its arguments. Hence, for every
should behave in a controlled manner the corresponding range of the function needs to behave controlled in relation to its arguments. Hence, for every ![]() a corresponding
a corresponding ![]() needs to exist as outlined in the definition.
needs to exist as outlined in the definition.
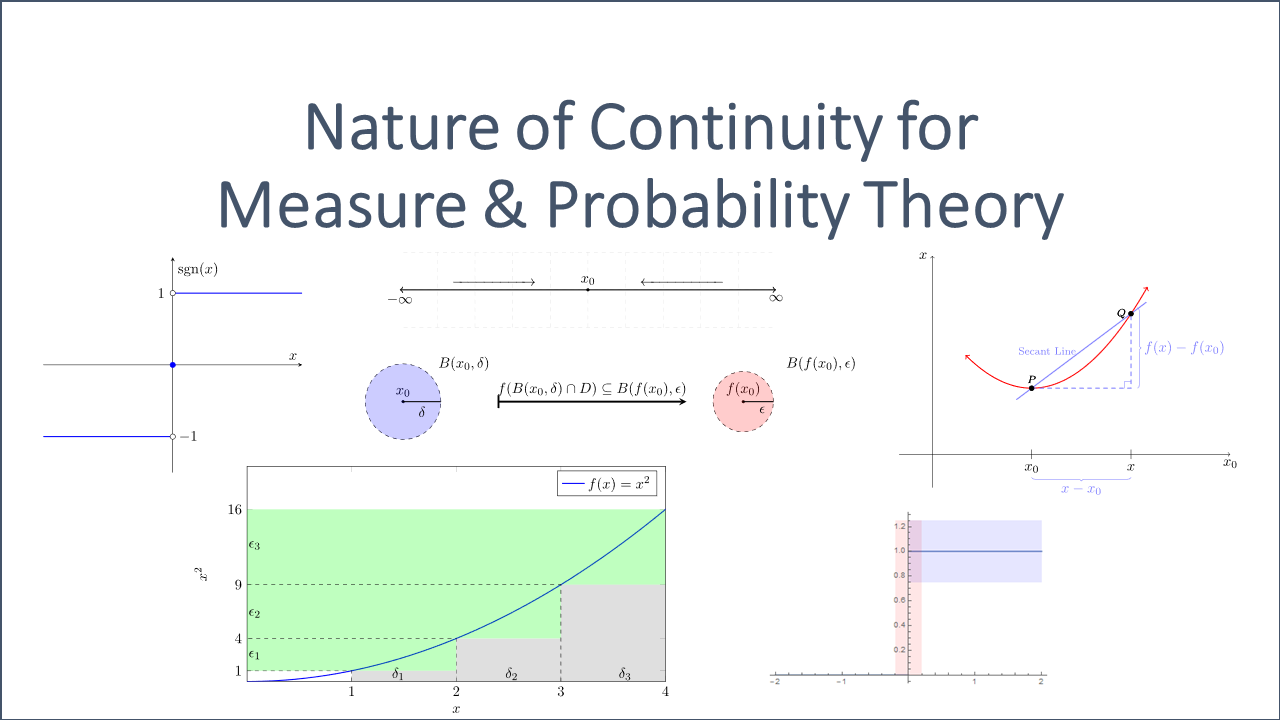
We can also use balls to provide an equivalent formulation.
A function ![]() is continuous at
is continuous at ![]() if and only if, for every
if and only if, for every ![]() , there is a
, there is a ![]() such that
such that ![]() .
.
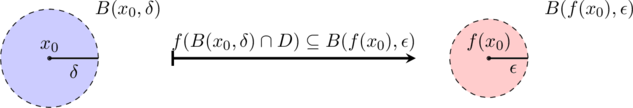
We can even go further and formulate continuity in terms of neighborhoods:
A function ![]() with domain
with domain ![]() is continuous at
is continuous at ![]() if and only if, for every neighborhood
if and only if, for every neighborhood ![]() of
of ![]() , there is a neighborhood
, there is a neighborhood ![]() of
of ![]() such that
such that ![]() .
.
We can use one of the equivalent formulation of continuity to double-check whether a function is continuous at a point.
Check for Continuity at a point:
One has to conduct several steps to double-check whether a function ![]() is continuous at a given point
is continuous at a given point ![]() :
:
- Set
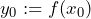 ;
; - Consider an arbitrary ball
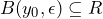 around the image point if you want to prove that
around the image point if you want to prove that 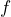 is continuous at
is continuous at 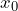 . If you think that
. If you think that 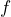 is not continuous try to find a suitable ball to contradict the definition in the next step;
is not continuous try to find a suitable ball to contradict the definition in the next step; - Check whether there is a corresponding ball
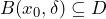 such that
such that 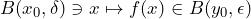 . If for some fixed
. If for some fixed 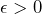 no such ball can exist, then the function
no such ball can exist, then the function 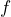 at
at 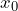 is not continuous.
is not continuous.
Another way of better understanding the definition is to consider what it means if a function ![]() is NOT continuous at a point
is NOT continuous at a point ![]() .
.
According to the Definition 2.1 this would mean that there must be an ![]() (sometimes called ‘loser’
(sometimes called ‘loser’ ![]() ) with the property that, for each
) with the property that, for each ![]() , there are
, there are ![]() such that
such that
![]()
Let us consider some examples to illustrate the definition of continuity at a point further.
Example 2.1 (Constant Function):
The constant functions ![]() with
with ![]() is continuous at every point in the domain
is continuous at every point in the domain ![]() . Let
. Let ![]() be a bounded subset.
be a bounded subset.
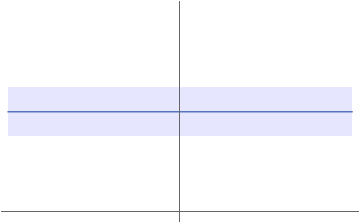
 tube around
tube around Let ![]() and let
and let ![]() be an arbitrary ball around the only image point
be an arbitrary ball around the only image point ![]() . We can choose
. We can choose ![]() to be an arbitrarily (large) positive real figure such as
to be an arbitrarily (large) positive real figure such as ![]() , then the following holds true:
, then the following holds true:
![]()
for any ![]() . Given that any point of the domain will always be mapped on
. Given that any point of the domain will always be mapped on ![]() the distance between the corresponding image points will always be zero.
the distance between the corresponding image points will always be zero.
If we pick a small ![]() instead, the implication above would still hold true since the implication from a wrong statement is always correct.
instead, the implication above would still hold true since the implication from a wrong statement is always correct.
Hence, the function ![]() is continuous on its domain.
is continuous on its domain.
![]()
Note that this type of continuity of ![]() at a point is by definition a local property:
at a point is by definition a local property:
If ![]() is an isolated point of the domain
is an isolated point of the domain ![]() (i.e. a point of
(i.e. a point of ![]() which is not an accumulation point of
which is not an accumulation point of ![]() ), then every function
), then every function ![]() defined at
defined at ![]() will be continuous at
will be continuous at ![]() . The reason is quite simple: for a sufficiently small
. The reason is quite simple: for a sufficiently small ![]() there is only one
there is only one ![]() satisfying
satisfying ![]() , namely
, namely ![]() , and
, and ![]() .
.
The following example shows why jumps are usually not compatible with continuity.
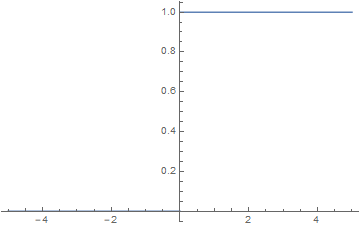
Example 2.2 (Heavyside Function):
Let us consider the so-called Heavyside Function ![]() defined via
defined via
(2) 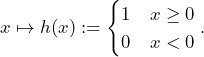
Constant functions are continuous as shown in Example 2.1. In addition, continuity is a local property which is why we can restrict our focus to the point ![]() since there is a jump in the graph from 0 to 1.
since there is a jump in the graph from 0 to 1.
The set ![]() is a ball of
is a ball of ![]() . Note that the image set of
. Note that the image set of ![]() only contains
only contains ![]() and
and ![]() .
.

 – and
– and 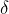 ball showing non-continuity at
ball showing non-continuity at 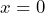
There cannot be a ball ![]() of the domain, such that
of the domain, such that ![]() since there must be a negative
since there must be a negative ![]() that will be mapped to 0 via
that will be mapped to 0 via ![]() . Apparently,
. Apparently, ![]() , which is why the Heaviside function is not continuous at zero but continuous everywhere else.
, which is why the Heaviside function is not continuous at zero but continuous everywhere else.
![]()
Maybe you want to have a look on the second part of the following video by 3Blue1Brown where limits and the ![]() –
–![]() definition is explained.
definition is explained.
Theorem 2.1 (Limits & Continuity):
Let ![]() be a function from one metric space
be a function from one metric space ![]() to the metric space
to the metric space ![]() . Then
. Then ![]() is continuous at
is continuous at ![]() if, and only if, for every sequence
if, and only if, for every sequence ![]() in
in ![]() convergent to
convergent to ![]() , the corresponding sequence
, the corresponding sequence ![]() in
in ![]() converges to
converges to ![]() , i.e.
, i.e.
(3) ![]()
![]()
Hence, continuity can also be interpreted as convergence-preserving.
Proof:
Let ![]() be continuous at
be continuous at ![]() and let
and let ![]() be a convergent sequence to
be a convergent sequence to ![]() . Due to the continuity the following holds:
. Due to the continuity the following holds:
![]()
This, however, already implies the convergence of ![]() to
to ![]() since
since ![]() gets arbitrarily close to
gets arbitrarily close to ![]() .
.
Let us now assume that for every convergent sequence ![]() the following holds:
the following holds:
(4) ![]()
Let us further assume that ![]() is not continuous at
is not continuous at ![]() . This means that there exists a ball
. This means that there exists a ball ![]() around
around ![]() such that we cannot find a
such that we cannot find a ![]() with
with ![]() . That is, there is an
. That is, there is an ![]() (that corresponds with the ball
(that corresponds with the ball ![]() ), such that for all
), such that for all ![]()
![]() . Let us now consider the balls
. Let us now consider the balls ![]() for the convergent sequence
for the convergent sequence ![]() with
with ![]() . However, we cannot find a
. However, we cannot find a ![]() (or equivalent an integer
(or equivalent an integer ![]() ) with
) with ![]() . This means that
. This means that ![]() does not converge to
does not converge to ![]() since the ball
since the ball ![]() would not contain any element. This contradicts the initial assumption (4) and proves the assertion.
would not contain any element. This contradicts the initial assumption (4) and proves the assertion.
![]()
At last, we will also look into global properties of continuous functions.
Theorem 2.2 (Continuity & Open Sets):
Let ![]() be a function from one metric space
be a function from one metric space ![]() to the metric space
to the metric space ![]() . Then
. Then ![]() is continuous on
is continuous on ![]() if, and only if,
if, and only if, ![]() for every open set
for every open set ![]() in
in ![]() .
.
![]()
Continuity therefore preserves open sets. This should not be a big surprise since limits can also be expressed using open sets (e.g. balls).
Proof:
Suppose ![]() is continuous on
is continuous on ![]() and
and ![]() is an open set in
is an open set in ![]() . We have to show that every point of
. We have to show that every point of ![]() is an interior point of
is an interior point of ![]() . Suppose
. Suppose ![]() and
and ![]() . Since
. Since ![]() is open, there exists an
is open, there exists an ![]() such that
such that ![]() if
if ![]() . Applying the continuity of
. Applying the continuity of ![]() at
at ![]() we know that there exists a
we know that there exists a ![]() such that
such that ![]() if
if ![]() . Hence,
. Hence, ![]() as soon as
as soon as ![]() .
.
Conversely, suppose that ![]() is open in
is open in ![]() for every open set
for every open set ![]() in
in ![]() . Fix
. Fix ![]() and
and ![]() , let
, let ![]() be the set of all
be the set of all ![]() such that
such that ![]() . Since
. Since ![]() is open
is open ![]() is also an open set. Hence, there exists a
is also an open set. Hence, there exists a ![]() such that
such that ![]()
![]() .
.
This completes the proof.
![]()
One-Sided Continuity
The following video introduces continuity at a point on the real line by using limits (from the left and right). Hence, it might serve as a nice warm-up for this section.
Let us restrict in this section to the metric space ![]()
Definition 3.1 (Left- & Right-Continuous)
Let ![]() and
and ![]() . Let
. Let ![]() . If
. If ![]() is continuous at
is continuous at ![]() as a function on
as a function on ![]() , we say it is right-continuous at
, we say it is right-continuous at ![]() .
.
Let ![]() and
and ![]() . Let
. Let ![]() . If
. If ![]() is continuous at
is continuous at ![]() as a function on
as a function on ![]() , we say it is left-continuous at
, we say it is left-continuous at ![]() .
.
![]()
We can characterize both limit-types based on one-sided limits. Then, the definition of left- and right-continuity is equivalent to

and
, respectively.
In a 1-dimensional vector space such as ![]() , there are two possibilities to approach an element
, there are two possibilities to approach an element ![]() .
.

In a 2-dimensional space, however, it is possible to approach from infinite many directions since you can approach a point from any possible angle ![]() .
.
Continuity in multi-dimensions will be treated further below in this article. Hence, let us get back to the 1-dimensional metric space ![]() with
with ![]() as distance function.
as distance function.
Example 3.1 (Signum Function and One-Sided Continuity):
Let us consider the so-called Signum Function ![]() defined via
defined via
(5) 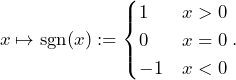
The domain of the function is the real line and the corresponding graph is shown as follows.
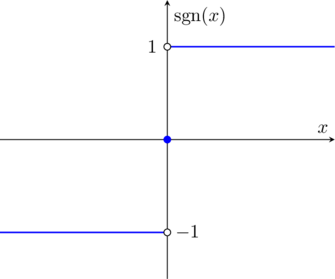
The ![]() function does not have a limit at
function does not have a limit at ![]() , because if you approach 0 from the right the value is 1 while if you approach from the left the value is -1. We then write
, because if you approach 0 from the right the value is 1 while if you approach from the left the value is -1. We then write ![]() and
and ![]() . The actual value at
. The actual value at ![]() is, however,
is, however, ![]() .
.
Note that the definition ![]() makes the signum function continuous from neither side at
makes the signum function continuous from neither side at ![]() , but a different convention would allow us to have one or the other but not both.
, but a different convention would allow us to have one or the other but not both.
![]()
Example 3.1 illustrated that there might be different types of discontinuities. There are three kinds of discontinuities at a point ![]() :
:
- Removable Discontinuity:
If one-sided limit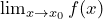 exists and is finite and can be removed by re-defining the function. That is, the function is either undefined at
exists and is finite and can be removed by re-defining the function. That is, the function is either undefined at  or
or  .
. - Jump or Step Discontinuity:
If one-sided limit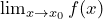 exists and is finite but not equal. It is not possible to re-define the function such that the one-sided limits are all the same.
exists and is finite but not equal. It is not possible to re-define the function such that the one-sided limits are all the same. - Infinite or Essential Discontinuity:
If one-sided limits do not exist or are infinite.
Please also refer to the classification of singularities, where it is about differentiability of (complex) functions. Both classifications are related to each other closely.
Let us illustrate this classification of discontinuities by looking at specific examples.
Example 3.2 (Classification of Discontinuities):
a) Consider the function
![]()
which is not defined at ![]() as illustrated in the next graph.
as illustrated in the next graph.

Apparently, this discontinuity is a removable one since we can simply extend or change the definition of ![]() such that
such that ![]() .
.
b) Let us now re-consider the Heavyside Function of Example 2.2, which has a jump discontinuity at ![]() . It has
. It has ![]() and
and ![]() as its left- and right-sided limit. In its graph we can clearly see a jump.
as its left- and right-sided limit. In its graph we can clearly see a jump.
c) An essential or infinite discontinuity is of a very different kind. Consider the following well-known function
![]()
and its graph
The limit from the left ![]() and the limit from the right
and the limit from the right ![]() are not consistent with each other. Hence, it is an essential or infinite discontinuity.
are not consistent with each other. Hence, it is an essential or infinite discontinuity.
![]()
Note that monotone functions can only have countable many jump discontinuities.
The following theorem outlines the interlinkage between continuous at a point and one-sided continuity at the same point.
Theorem 3.1 (Left- & Right-Continuous & Continuity)
The function ![]() is continuous at
is continuous at ![]() if and only if it is both right- and left-continuous at
if and only if it is both right- and left-continuous at ![]() .
.
Proof:
‘![]() ‘ If the function is continuous on its domain
‘ If the function is continuous on its domain ![]() , it means that
, it means that ![]() with
with ![]() implies
implies ![]() . This holds true for
. This holds true for ![]() and
and ![]() . Hence, left- and right-sided continuity follows.
. Hence, left- and right-sided continuity follows.
‘![]() ‘ Assume that
‘ Assume that ![]() is left and right-continuous.
is left and right-continuous.
Let further ![]() denote a sequence
denote a sequence ![]() with
with ![]() . Suppose
. Suppose ![]() does not converge to
does not converge to ![]() , which would contradict continuity. Then there must be an
, which would contradict continuity. Then there must be an ![]() such that for all
such that for all ![]() and corresponding
and corresponding ![]() the following holds true:
the following holds true:
![]() .
.
In other words, we cannot find any ![]() such that all terms
such that all terms ![]() with
with ![]() are arbitrarily close to the value
are arbitrarily close to the value ![]() . This, however, implies that either there exists infinitely many terms of the sequence with
. This, however, implies that either there exists infinitely many terms of the sequence with ![]() , or infinitely many with
, or infinitely many with ![]() such that
such that ![]() . In either case, there exists a subsequence
. In either case, there exists a subsequence ![]() ,
, ![]() with all terms in only one of
with all terms in only one of ![]() or
or ![]() , such that
, such that ![]() for
for ![]() . But such a sequence violates the assumption that
. But such a sequence violates the assumption that ![]() is left and right continuous. Hence, the function must be continuous at
is left and right continuous. Hence, the function must be continuous at ![]() .
.
The following is an alternative and much more elegant proof of the reverse direction.
‘![]() ‘ Let
‘ Let ![]() . By the left and right continuity of
. By the left and right continuity of ![]() at
at ![]() , there are positive numbers
, there are positive numbers ![]() such that
such that ![]() for all
for all ![]() and
and ![]() . Set
. Set ![]() . Then
. Then ![]() for all
for all ![]() . Therefore,
. Therefore, ![]() is continuous at
is continuous at ![]() .
.
![]()
Let ![]() continuous on
continuous on ![]() and let further
and let further ![]() be a limit point of
be a limit point of ![]() . If
. If ![]() is not closed, then
is not closed, then ![]() may not be in
may not be in ![]() and so
and so ![]() is not defined at
is not defined at ![]() . In the following we consider whether
. In the following we consider whether ![]() can be defined so that
can be defined so that ![]() is continuous on
is continuous on ![]() .
.
If such an extension exists, then, for any sequence ![]() in
in ![]() , which converges to
, which converges to ![]() , the corresponding sequence
, the corresponding sequence ![]() converges to
converges to ![]() . Thus, for a (not necessarily continuous) function
. Thus, for a (not necessarily continuous) function ![]() and a limit point
and a limit point ![]() , we define
, we define
![]()
provided that for each convergent sequence ![]() in
in ![]() , the corresponding sequence
, the corresponding sequence ![]() also converges in
also converges in ![]() .
.
Proposition 3.1 (Neighborhoods and Converging Functions)
The following are equivalent:
(i) ![]() ;
;
(ii) For each neighborhood ![]() of
of ![]() in
in ![]() , there is a neighborhood
, there is a neighborhood ![]() of
of ![]() in
in ![]() such that
such that ![]() .
.
Proof: ‘(i) ![]() (ii)’ Suppose that there is a neighborhood
(ii)’ Suppose that there is a neighborhood ![]() of
of ![]() in
in ![]() such that
such that ![]() for each neighborhood
for each neighborhood ![]() of
of ![]() in
in ![]() . Consider the sequence of open balls
. Consider the sequence of open balls
![]()
,![]() , in the complement set
, in the complement set ![]() . We can chose
. We can chose ![]() from
from ![]() to create a sequence, which is in
to create a sequence, which is in ![]() and converges to
and converges to ![]() . However, all terms of
. However, all terms of ![]() are not contained in
are not contained in ![]() and thus
and thus ![]() cannot converge to
cannot converge to ![]() .
.
‘(ii) ![]() (i)’ Let
(i)’ Let ![]() be a sequence in
be a sequence in ![]() such that
such that ![]() in
in ![]() , and
, and ![]() a neighborhood of
a neighborhood of ![]() in
in ![]() . By hypothesis, there is some neighborhood
. By hypothesis, there is some neighborhood ![]() of
of ![]() such that
such that ![]() . Since
. Since ![]() converges to
converges to ![]() , there is some
, there is some ![]() such that
such that ![]() for all
for all ![]() . Thus, the image sequence
. Thus, the image sequence ![]() is contained in
is contained in ![]() for all
for all ![]() . This means that
. This means that ![]() .
.
![]()
Uniform Continuity
Suppose ![]() and
and ![]() with
with ![]() and
and ![]() metric spaces. Assume that
metric spaces. Assume that ![]() is continuous on its domain
is continuous on its domain ![]() : for any point
: for any point ![]() and any
and any ![]() , there is a corresponding
, there is a corresponding ![]() , such that
, such that
![]()
for any ![]() .
.
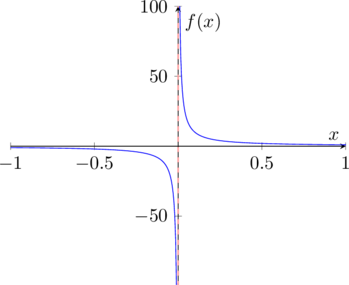
In general, ![]() depends on the chosen
depends on the chosen ![]() and the point
and the point ![]() as we can see in the following chart of the function
as we can see in the following chart of the function ![]() for the domain
for the domain ![]() .
.
Even though ![]() the corresponding
the corresponding ![]() tubes with
tubes with ![]() range from
range from ![]() to
to ![]() in the illustrative graph above. This in return means, that for a given
in the illustrative graph above. This in return means, that for a given ![]() not an unique
not an unique ![]() would do the job for the entire positive real line. However, if the domain of
would do the job for the entire positive real line. However, if the domain of ![]() is bounded, we can find a
is bounded, we can find a ![]() depending on a given
depending on a given ![]() such that a specific continuity is ensured. For more details please refer to Example 4.1 d) and Example 4.2.
such that a specific continuity is ensured. For more details please refer to Example 4.1 d) and Example 4.2.
In general, we therefore cannot expect that for a fixed ![]() the same value of
the same value of ![]() will serve equally well for every point
will serve equally well for every point ![]() . This might happen, however, and when it does, the function possesses the following properties.
. This might happen, however, and when it does, the function possesses the following properties.
Definition 4.1 (Uniformly Continuous):
Let ![]() be a function from one metric space
be a function from one metric space ![]() to another
to another ![]() . Then
. Then ![]() is said to be uniformly continuous on a subset
is said to be uniformly continuous on a subset ![]() of
of ![]() if for every
if for every ![]() there is a
there is a ![]() (depending only on
(depending only on ![]() ), such that
), such that
![]()
for all ![]() . Note that
. Note that ![]() is not fixed.
is not fixed.
![]()
Example 4.1 (Uniform Continuity):
a) The function ![]() ,
, ![]()
![]()
is continuous but not uniformly continuous on its domain.
Since ![]() is the restriction of a rational function, it is certainly continuous.
is the restriction of a rational function, it is certainly continuous.
Set ![]() and suppose we could find a
and suppose we could find a ![]() to satisfy the definition of uniform continuity. Taking
to satisfy the definition of uniform continuity. Taking ![]() and
and ![]() , we obtain
, we obtain ![]() and
and
![]()
Hence, for these two points we would always have ![]() , contradicting the definition of uniform continuity.
, contradicting the definition of uniform continuity.
b) Let us continue Example 2.1 and re-consider the class of the constant functions. A constant function on a bounded subset ![]() is uniformly continuous since we can pick one
is uniformly continuous since we can pick one ![]() that works for all
that works for all ![]() as outlined in Example 2.1.
as outlined in Example 2.1.
c) Let ![]() defined by
defined by ![]() . This function is continuous and uniformly continuous on the standard metric space
. This function is continuous and uniformly continuous on the standard metric space ![]() . To prove this, let
. To prove this, let ![]() , and set
, and set ![]() . Then for every
. Then for every ![]() there is a
there is a ![]() (depending only on
(depending only on ![]() ), such that
), such that
![]()
for all ![]() . Note that
. Note that ![]() is not fixed.
is not fixed.
d) Let ![]() defined by
defined by ![]() . At the beginning of this section, we illustrated that the quadratic function
. At the beginning of this section, we illustrated that the quadratic function ![]() is not uniformly continuous on the entire real line. Now, we formally prove it: Suppose
is not uniformly continuous on the entire real line. Now, we formally prove it: Suppose ![]() and suppose that
and suppose that ![]() is uniformly continuous. For all
is uniformly continuous. For all ![]() and
and ![]() , we would find that
, we would find that
![]()
for any real ![]() . However, this would imply
. However, this would imply
![]()
which is a contradiction since we can choose ![]() large.
large.
We will see that the same function is uniformly continuous on specific (bounded) subsets.
![]()
Uniform continuity on a set ![]() implies continuity on
implies continuity on ![]() . The converse is also true if the set
. The converse is also true if the set ![]() is compact.
is compact.
Theorem 4.1 (Heine, Continuous Functions on Compact Sets)
Suppose that ![]() is a function from a metric spaces
is a function from a metric spaces ![]() to another
to another ![]() . Let
. Let ![]() be a compact set and assume that
be a compact set and assume that ![]() is continuous on
is continuous on ![]() . Then
. Then ![]() is uniformly continuous on
is uniformly continuous on ![]() .
.
That is, continuous functions on compact sets are uniformly continuous.
Proof: Let ![]() be given. Then each point
be given. Then each point ![]() has associated with it a ball
has associated with it a ball ![]() , with
, with ![]() depending on
depending on ![]() , such that
, such that
![]()
whenever ![]() .
.
Consider the collection of balls ![]() for each
for each ![]() with radius
with radius ![]() . These open balls cover
. These open balls cover ![]() and, since
and, since ![]() is compact, a finite number
is compact, a finite number ![]() of them also cover
of them also cover ![]() , say
, say
In any ball of twice the radius, ![]() , we have
, we have
![]()
whenever ![]() . Let
. Let ![]() be the smallest of the numbers
be the smallest of the numbers ![]() . We show that this
. We show that this ![]() works for the definition of uniform continuity. For this purpose, consider two points of
works for the definition of uniform continuity. For this purpose, consider two points of ![]() , say
, say ![]() and
and ![]() with
with ![]() . By the above discussion there is some ball
. By the above discussion there is some ball ![]() containing
containing ![]() , so
, so ![]() . By the triangle inequality we have
. By the triangle inequality we have
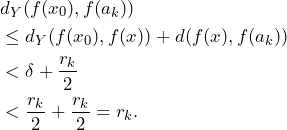
Hence, ![]() , so we also have
, so we also have ![]() . Using the triangle inequality once more we find
. Using the triangle inequality once more we find
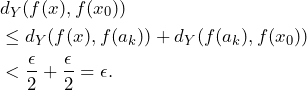
![]()
In general, the function ![]() defined by
defined by ![]() is not uniformly continuous. However, if we restrict the function to a bounded closed subset the situation is different.
is not uniformly continuous. However, if we restrict the function to a bounded closed subset the situation is different.
Example 4.2 (Uniform Continuity on Compact Sets):
The function ![]()
![]()
is continuous and uniformly continuous on its bounded and closed domain ![]() . To prove this, observe that
. To prove this, observe that
![]()
for ![]() . Thus, if
. Thus, if ![]() , then
, then ![]() . If
. If ![]() is given we only need to take
is given we only need to take ![]() to guarantee that
to guarantee that ![]() for every pair
for every pair ![]() with
with ![]() . This shows that
. This shows that ![]() is uniformly continuous on
is uniformly continuous on ![]() .
.
![]()
Lipschitz & Hölder Continuity
The next type of continuity is named after the German mathematician Rudolf Lipschitz.
Definition 5.1 (Lipschitz Continuity):
Let ![]() be a function from one metric space
be a function from one metric space ![]() to another
to another ![]() . Then
. Then ![]() is said to be Lipschitz continuous on
is said to be Lipschitz continuous on ![]() if there exists a positive real number
if there exists a positive real number ![]() (which may depend on
(which may depend on ![]() ) such that
) such that
(6) ![]()
whenever ![]() and
and ![]() .
.
![]()
Think about why the constant ![]() needs to be positive?
needs to be positive?
The inequality contains only absolute values, which is why a change of sign is not possible. Because of a similar reason, the constant ![]() cannot be zero since the product would be zero as well.
cannot be zero since the product would be zero as well.
The so-called Lipschitz condition (6) is also important in other areas of Analysis (e.g. differential equations) and Measure Theory (e.g. geometric measure theory or nonlinear expectations).
A Lipschitz continuous function ![]() on
on ![]() is (uniformly) continuous: Let
is (uniformly) continuous: Let ![]() be Lipschitz continuous, which means that there is a
be Lipschitz continuous, which means that there is a ![]() such that
such that ![]() for all
for all ![]() . Let
. Let ![]() and set
and set ![]() , then we can imply for any
, then we can imply for any ![]() with
with ![]() that
that ![]() . Note that the
. Note that the ![]() is not dependent on
is not dependent on ![]() .
.
![]()
Let us consider two very simple examples.
Example 5.1 (Lipschitz Continuity):
a) The identity ![]() defined by
defined by ![]() is Lipschitz continuous on
is Lipschitz continuous on ![]() . To prove this, observe that
. To prove this, observe that
![]()
which holds true for any constant ![]() .
.
b) The absolute value function ![]() is Lipschitz continuous on
is Lipschitz continuous on ![]() . To prove this, observe that
. To prove this, observe that
![]()
due to the reverse triangle inequality. Hence, we can choose ![]() as Lipschitz constant. Note, however, that the absolute value function is not differentiable at
as Lipschitz constant. Note, however, that the absolute value function is not differentiable at ![]() .
.
![]()
Lipschitz continuity in ![]() means that
means that
![]()
which is the amount of the secant increase is limited by ![]() .
.
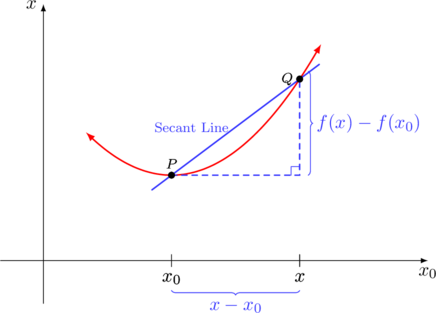
A generalization of Lipschitz continuity is named after another German mathematician Otto Hölder.
Definition 5.2 (Hölder Continuity):
Let ![]() be a function from one metric space
be a function from one metric space ![]() to another
to another ![]() . Then
. Then ![]() is said to satisfy a Hölder condition of order
is said to satisfy a Hölder condition of order ![]() if there exists a positive real number
if there exists a positive real number ![]() (which may depend on
(which may depend on ![]() ) and an exponent
) and an exponent ![]() such that
such that
![]()
whenever ![]() .
.
![]()
Lipschitz continuous functions are Hölder continuous with exponent ![]() since Hölder continuity is a generalization of Lipschitz continuity. Hence, Hölder continuous functions are in general not Lipschitz continuous.
since Hölder continuity is a generalization of Lipschitz continuity. Hence, Hölder continuous functions are in general not Lipschitz continuous.
A Hölder continuous function ![]() is (uniformly) continuous with Lipschitz constant
is (uniformly) continuous with Lipschitz constant ![]() and exponent
and exponent ![]() : let
: let ![]() and set
and set ![]() (only dependent on
(only dependent on ![]() ) , then we got for all
) , then we got for all ![]() with
with ![]()
![]()
Note that ![]() does not depend on
does not depend on ![]() .
.
![]()
Example 5.2 (Hölder Continuity):
The root function ![]() defined by
defined by ![]() is Hölder but not Lipschitz continuous on
is Hölder but not Lipschitz continuous on ![]() . Let
. Let ![]() and without loss of generality
and without loss of generality ![]() , then
, then
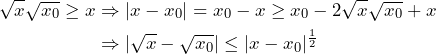
The second statement that the root function is not Lipschitz continuous can be concluded as follows: Assume there is a Lipschitz constant ![]() such that
such that ![]() for all
for all ![]() . If we then choose
. If we then choose ![]() we get
we get ![]() and thus
and thus ![]() for all
for all ![]() , which contradicts the existence of
, which contradicts the existence of ![]() .
.
![]()
Literature:
[1]
[2]
[3]