In this post, an introduction to decision-making under risk and uncertainty is provided. To this end, basic concepts and components of a decision-making problem are explained and illustrated. Preference relations of a decision maker as well as corresponding utility functions are outlined and put into context.
Decision theory but also related game theory can offer perspectives on how a decision maker should act under various circumstances to obtain a maximum of utility, see [7]. The theory can generate answers and other useful information to maximize utility, or, in the case of the entrepreneur, profit.
In particular, modern game theory can offer models that are capable to handle high degrees of uncertainty much better than classical probability or measure theory, see [2].
Overview on the Topic by Itzhak Gilboa
Itzhak Gilboa provides a quite good overview on the subject in the following video, which might serve as an introduction to the topic:
There is also a rather non-technical corresponding free eBook – Theory of Decision under Uncertainty by Itzahk Gilboa available. It explains many concepts also discussed and studied in the present post.
What is Decision Theory and How is it Related to Other Theories?
Decision theory deals with situations in which one or more actors have to make choices among given alternatives. Decision-making is considered to be a cognitive process resulting in the selection of a belief or a course of action among several alternative possibilities. Decision theory is also sometimes called theory of choice.
Decision theory provides a means of handling the uncertainty involved in any decision-making process. If enough information is available, uncertainty with respect to the outcomes might be handled by condensing a probability distribution and maximizing so-called “expected utility”. However, there are also situations, where the degree of uncertainty is too high to come up with a reasonable distribution assumption. Game theory provides theoretical frameworks for modeling both types.
Decision theory is closely related to modern game theory, which itself has a lot of interconnections to so-called theory of capacities (also refer to [1] and [2]). Latter theory is a possible framework that can be applied to situations with a high degree of uncertainty.
Decision theory is also applied in artificial intelligence. This holds also true for the concepts of capacity (note that belief functions are special capacities) and uncertainty. Both concepts will be outlined below.
Components of a Decision Problem
A decision problem is a situation, where a decision maker (in this context also called agent) has to make a choice between several actions. The outcomes/consequences ![]() of each action depends on the states of nature
of each action depends on the states of nature ![]() . An action can therefore be represented by a function
. An action can therefore be represented by a function ![]() , which assigns a consequence
, which assigns a consequence ![]() to each state
to each state ![]() . That is, the outcome of an action is in general uncertain and it depends on the states of nature.
. That is, the outcome of an action is in general uncertain and it depends on the states of nature.
An illustrative example is a betting on a horse race: imagine that ten different horses start at a horse race. The states of nature ![]() is the set of horses, consequences
is the set of horses, consequences ![]() are amounts of money ranging from a loss (of the ticket price) to a win. An action is a representation of a bet taken by a decision maker.
are amounts of money ranging from a loss (of the ticket price) to a win. An action is a representation of a bet taken by a decision maker.
The states of nature ![]() reflect the potential scenarios that might be realized going forward. It is uncertain which state is the true one. The states of nature describe the real-world process that generates the uncertainty.
reflect the potential scenarios that might be realized going forward. It is uncertain which state is the true one. The states of nature describe the real-world process that generates the uncertainty. ![]() is assumed to be exhaustive. That is, the true but unknown state of nature should belong to
is assumed to be exhaustive. That is, the true but unknown state of nature should belong to ![]() . Sometimes, this is also called closed world assumption. The decision maker does not have any influence on which state is true. States of nature are endowed with a
. Sometimes, this is also called closed world assumption. The decision maker does not have any influence on which state is true. States of nature are endowed with a ![]() -algebra
-algebra ![]() in the continuous case, whereas
in the continuous case, whereas ![]() denotes the power set
denotes the power set ![]() in the discrete case.
in the discrete case.
Regarding the horse race example, it is required that ![]() contains the winning horse since every horse corresponds to a world in which this horse will win the race. A priori it is not clear which horse is going to win and the decision maker has no influence on the outcome of the race.
contains the winning horse since every horse corresponds to a world in which this horse will win the race. A priori it is not clear which horse is going to win and the decision maker has no influence on the outcome of the race.
Subsets of ![]() are called events and the elements of the set
are called events and the elements of the set ![]() are mutually exclusive as only one of them can realize.
are mutually exclusive as only one of them can realize.
A typical decision problem within finance is to decided how to invest regarding an universe of potential assets. The states of nature are the asset price developments regarding the relevant time horizon, the investment sizes, etc. Acts reflect the selection of a portfolio and the consequences could comprise corresponding profits and losses and risk figures.

Outcomes/consequences are mostly real numbers. However, the potential outcome can also be any other set.
For instance, when you are leaving the house in the morning without an umbrella and the weather forecast predicted rain, possible consequences might be that you get wet or that you might have to find cover from the rain, and, thus being late in the evening. The states of nature ![]() reflect the possible weather conditions (sunny, heavy rain, rainy, etc.) and other related circumstances.
reflect the possible weather conditions (sunny, heavy rain, rainy, etc.) and other related circumstances.
We furthermore assume in the following, that the consequences ![]() are quantifiable and thus are represented by the real numbers
are quantifiable and thus are represented by the real numbers ![]() . The set of all actions
. The set of all actions ![]() comprise a space of functionals. A functional is special function, where the range is simply a real number. The functional space becomes important when it is about the integrals of
comprise a space of functionals. A functional is special function, where the range is simply a real number. The functional space becomes important when it is about the integrals of ![]() .
.
Next, let us discuss what types of interpretations of probability exist. This will be fruitful in the subsequent study of risk vs. uncertainty.
What is Probability?
There is no unique answer to the question of what probability actually is. Nonetheless, let us consider some (intuitive) thoughts about probabilities:
- It is about an event or a situation, where the outcome is random and therefore not known a priori.
- Randomness might be the lack of pattern or predictability in events and situations.
- Probabilities should reflect the likelihoods of specific events. That is, a certain degree of knowledge about the events is needed. Otherwise, we would not be able to determine the probabilities.
Let us now discuss what features events/situations need to have, such that they can be studied using probabilities. What about real-world situations such as gambling games or other repeatable real-world events with stable conditions?
Gambling games can be modeled with a well-defined experiment since the scope and its conditions are stable. In addition, the outcome of one game (e.g. rolling dices) does usually not affect other games, i.e., they are usually independent. Games can usually be repeated arbitrarily often and they can easily be simulated. If the games are conducted properly, the interpretation of the outcomes of many games should be objective to a certain degree.
A frequentist would interpret a probability as the limit of its relative frequency in a large number of trials. This interpretation stresses the importance of experimental science (e.g. experimental physics) and it is ultimately based on the law of large numbers. Note, however, that relative frequencies cannot serve as a definition of the concept of probability to begin with. The law of large number already uses the concept of probability, thus, the limit of relative frequencies cannot be used to define it. Instead, the scope conditions (i.e. Kolmogorov Axioms) are used, such that probability concepts such as the law of large numbers are valid and can be applied.
There are of course also situations / events, that cannot be repeated / recreated under the same conditions. A financial crisis, for example, is by nature an one-off event and can therefore not be repeated under the same conditions. The global financial crisis that erupted around 2007 has had a huge impact on politics and financial regulation and thus will likely affect subsequent future crises (i.e. the events are not independent). And even if you think about several similar crises as independent realization of the same random variable, the data basis would most likely still be too small to derive any sensible conclusion from it.
An alternative approach is therefore to interpret probability as subjective beliefs. That is, a probability does not describe a property of an event but rather the subjective beliefs about it. Financial experts could be asked how likely they think it is that another financial crisis will happen going forward. Probability theory is then used to model and to update beliefs using new evidence and Bayes Theorem. However, also Bayesian statistics cannot deal with a too high level of uncertainty (refer to [2]). Please also refer to the Belief functions: past, present and future by Cuzzolin at Harvard Statistics. Cuzzolin explains potential difficulties, that may arise when Bayesian statistics is used, and he also outlines why belief functions (i.e. specific capacities) might work better.
There are also other theoretical/philosophical situations such as Pascal’s wager, where relative frequencies cannot exist.
In the following section we are going to explore what uncertainty actually is and how it is related to the concept of risk.
What is Uncertainty and Risk?
The general term uncertainty covers many aspects. Unknown states of natures, unknown probabilities, preferences of the decision maker, and many other things that are not yet known (i.e. unknown unknowns).
F. H. Knight first distinguished in 1921 between ‘risk’ and ‘uncertainty’ in his seminal book [4]. On the one hand, Knightian or complete uncertainty may be characterized as the complete absence of information or knowledge about a situation or an outcome of an event. Knightian risk, on the other hand, may be characterized as a situation, where the true information on the probability distribution is available. In practice, no parameter or distribution can be known for sure a priori. Hence, we find it preferable to think about degrees of uncertainty.

Coming back to gambling – discrete probability theory and combinatorics were conceived in the 16th and 17th century by mathematicians attempting to solve gambling problems (see [3]). Due to the fact that conditions of gambling games are well-known and stable, the degree of uncertainty is comparatively low. Good (but not prefect) estimates of the corresponding (objective) probability distributions are known. In such cases, classical probability theory and/or the classical measure theory are the right tools to tackle these types of problems. Note that even gambling games are subject to a certain degree of uncertainty. For instance, a die might be biased since it is not (and cannot be produced) perfectly symmetric.
Financial markets are complex systems involving human behavior and herd behavior. That is, financial markets are usually subject to a high level of uncertainty. Corresponding financial risks such as market or credit risk are therefore hard to guess. Important conditions such as the economic environment, financial regulations as well as the political landscape change over time. Hence, we might be able to observe a stock price on a regular basis, however, under very different circumstances. In addition, scarcity of data is quite common in finance (e.g. default-related data of companies, i.e. PDs or LGDs).
All results from a high-degree of uncertainty can be applied to risk, and results from risk can often be extended to situations with a high-degree of uncertainty.
An interesting standpoint is provided on Risk.net -Parameter und Modellrisiken in Risikoquantifizierungsmodellen (by Volker Bieta) on the models used in finance in a situation with high uncertainty.
Decision under Risk and Uncertainty
Given the uncertainty bearing on the states of nature ![]() , it is natural to endow
, it is natural to endow ![]() with a
with a ![]() -algebra
-algebra ![]() or a power set
or a power set ![]() depending on the cardinality of
depending on the cardinality of ![]() .
.
In order to supplement the spcae ![]() with a probability measure
with a probability measure ![]() an objective body of evidence needs to be available to estimate and test the corresponding distribution assumption. Decision-making based on objective information on the probability distribution over the states of nature is called decision under risk. Actions can then be seen as random variables (r.v.)
an objective body of evidence needs to be available to estimate and test the corresponding distribution assumption. Decision-making based on objective information on the probability distribution over the states of nature is called decision under risk. Actions can then be seen as random variables (r.v.) ![]() .
.
If no such objective information is available or if only subjective perception over the states of nature remains, the decision-making process is called decision under uncertainty. In such cases one must extend classical probability theory and deal with capacities, for instance. The probability resulting from the subjective perception is also known as subjective probability. Refer to [4].
Decision under risk can be seen everywhere in the literature and in finance. Modern game theory and its mathematical underlying -incl. the theory of capacities- should come to the forefront as a tool for decision makers, in particular, when complex problems need to be resolved and uncertainty is present.
In the review paper [2], the mathematical basics of uncertainty in finance is explained and put into context.
Preference Relation
Before we actually study subjective preferences, we would like to point out that there are markets, where preferences should not impact the price of a good. In a so-called complete market, the price of a contingent claim is fully determined by arbitrage arguments. Here, potential risks, that may influence utility and thus the preference relation of a decision maker can be perfectly hedged away. In an incomplete market, however, not all risks can be hedged and thus preference play a role in determining the price of a good. Please refer to the great book [6] for more details.
We assume that each decision maker has its own individual preferences, beliefs and desires about how the world is or should be. A decision maker’s preference relation effects its choices and need to be taken into consideration. Faced with two different consequences ![]() , a decision maker might prefer one over the other, that is,
, a decision maker might prefer one over the other, that is, ![]() . An element of
. An element of ![]() can be interpreted as a possible choice of the decision maker, that is,
can be interpreted as a possible choice of the decision maker, that is, ![]() contains the states of nature
contains the states of nature ![]() . In addition, it can also be identified with a suitable subset of all corresponding probability distribution (provided that there are known probability distributions).
. In addition, it can also be identified with a suitable subset of all corresponding probability distribution (provided that there are known probability distributions).
The relation between different preferences of a decision maker can be modeled using a binary relation ![]() with the following properties:
with the following properties:
- Asymmetry: If
 , then
, then  .
. - Negative transitivity: If
 and
and  , then either
, then either  or
or  or both must hold.
or both must hold.
This binary relation ![]() is called (strict) preference order or preference relation of the decision maker over
is called (strict) preference order or preference relation of the decision maker over ![]() . Hereby,
. Hereby, ![]() reads “
reads “![]() is preferred to
is preferred to ![]() ” . A binary relation can be used to compare two elements and is therefore actually a subset of
” . A binary relation can be used to compare two elements and is therefore actually a subset of ![]() .
.
Negative transitivity states that if a clear preference exists between two choices ![]() and
and ![]() , and if a third choice
, and if a third choice ![]() is added, then there is still a choice which is at least preferable (y if
is added, then there is still a choice which is at least preferable (y if ![]() ) or most preferable (
) or most preferable (![]() if
if ![]() ) [6].
) [6].

The term ‘negative transitivity’ becomes obvious considering the next characterization.
A relation ![]() is negatively transitive if, and only if,
is negatively transitive if, and only if,
(1) ![]()
Suppose that
A preference relation ![]() arranges the decision maker’s actions according to his/her preferences. It also induces a corresponding weak preference order
arranges the decision maker’s actions according to his/her preferences. It also induces a corresponding weak preference order ![]() defined by
defined by
![]()
and an indifference relation
![]()
The asymmetry together with the negative transitivity of ![]() are equivalent to the following two respective properties of
are equivalent to the following two respective properties of ![]() :
:
- Completeness: Either
 or
or  or both are true for all
or both are true for all  .
. - Transitivity: If
 and
and  , then
, then  for all
for all  .
.
Completeness of the weak preference order means that a decision maker is always capable of deciding between the alternatives ( ![]() or
or ![]() or both are true) presented. Transitivity tells us that if a decision maker considers
or both are true) presented. Transitivity tells us that if a decision maker considers ![]() at least as good as
at least as good as ![]() and
and ![]() at least as good as
at least as good as ![]() , then
, then ![]() is at least as good as
is at least as good as ![]() .
.
Let us have a closer look into why asymmetry and negative transitivity implies transitivity. To this end, assume that transitivity does not hold for a strict preference order. That is, suppose that ![]() and
and ![]() implies
implies ![]() . By asymmetry we infer
. By asymmetry we infer ![]() from
from ![]() . By (1) we have
. By (1) we have ![]() , which contradicts the first assumption regarding transitivity. Hence,
, which contradicts the first assumption regarding transitivity. Hence, ![]() must hold.
must hold.
A weak preference order can be split up into the corresponding asymmetric (![]() ) and symmetric (
) and symmetric (![]() ) part:
) part:
![]()
The indifference relation ![]() is an equivalence relation, that is, it is reflexive, symmetric and transitive. If we consider equivalence classes instead of single elements the discussion can be simplified without any loss of generalization.
is an equivalence relation, that is, it is reflexive, symmetric and transitive. If we consider equivalence classes instead of single elements the discussion can be simplified without any loss of generalization.
It is preferable to use functions instead of relations. A numerical representation of a preference order ![]() is a function
is a function ![]() such that
such that
![]()
With respect to the weak order, we have
![]()
Please note that such a numerical representation is not unique. For instance, if
Expected Value and Utility
But how shall we determine a preference relation?

Let us assume that a decision maker is presented the two lotteries as illustrated above. A lottery is a discrete distribution of probability on a (sub-)set of the states of nature ![]() . A naive approach is to use the expected value of the corresponding random variables to determine the preference of an individual. Then, one would prefer EUR 8.25mn = 0.75
. A naive approach is to use the expected value of the corresponding random variables to determine the preference of an individual. Then, one would prefer EUR 8.25mn = 0.75 ![]() EUR 11mn over EUR 8mn = 0.8
EUR 11mn over EUR 8mn = 0.8 ![]() EUR 10mn.
EUR 10mn.
This idea, however, seems not quite compatible with human behavior. Are utility and expected payoff (always) the same? There is no clear answer to this question as it actually depends on the individual.
The famous St. Petersburg Paradox [8] illustrates that many persons are rather risk avers:
- A fair coin is tossed repeatedly until it comes up heads for the first time. Let us say this happens on the
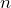 -th toss;
-th toss; - The payoff is then €
 ;
; - What is the most you would be willing to pay for this bet?
It turns out that the expected payoff of this bet is ![]() . The argument is that the payoff increases and the likelihood decreases at the same exponential pace. Let
. The argument is that the payoff increases and the likelihood decreases at the same exponential pace. Let ![]() be the likelihood that heads comes up first on the
be the likelihood that heads comes up first on the ![]() -th toss and
-th toss and ![]() is the corresponding payoff:
is the corresponding payoff:

Even though it is very unlikely that the first head comes up the first time, let us say, on the 1000-th toss, it is possible and contributes to the expected payoff with a huge amount of ![]() .
.
How much would you pay now that you know the expected monetary payoff is ![]() ?
?
Note that it is impossible to gain infinite wealth in real world since our resources are finite. In addition, one has to play the game very, very, … often to actually converge (in theory) towards infinity.
For most people their subjective utility (i.e. how much something matters to this individual) and the objective expected payoff diverge [8]. Usually, money has a declining marginal ‘utility’ and it is the expected utility (not the expected objective monetary payoffs) that rationality requires us to maximize provided that certain assumptions are met.
The following Vsauce2 video is also dedicated to the St. Peterburg Paradox and the expected utility theory.
In the following section it is assumed that the utility function ![]() of a decision maker is known.
of a decision maker is known.
Utility Functions and Decisions under Risk
Decisions under risk assumes that objective probabilities are known for all states of nature ![]() . That is, for each possible choice of the decision maker a corresponding probability distribution on a given subset of scenarios of
. That is, for each possible choice of the decision maker a corresponding probability distribution on a given subset of scenarios of ![]() exists. Hence, the set
exists. Hence, the set ![]() can be identified with a subset
can be identified with a subset ![]() of all probability spaces on
of all probability spaces on ![]() . In this context and provided that
. In this context and provided that ![]() is discrete, the probability spaces can also be identified with lotteries.
is discrete, the probability spaces can also be identified with lotteries.
For many individuals the expected value does not equal their subjective utility. Hence, the idea is to use a individual so-called utility function to personalize the value of the event and/or the situation. A utility function is a mapping ![]() , which quantifies the preference relation
, which quantifies the preference relation ![]() of the decision maker.
of the decision maker.

The larger ![]() the better from a point of view of the decision maker with utility function
the better from a point of view of the decision maker with utility function ![]() . For example, if
. For example, if ![]() are two possible consequences and
are two possible consequences and ![]() , then the consequence
, then the consequence ![]() is at least as good as
is at least as good as ![]() .
.
The St. Petersburg Paradox can be resolved by applying ![]() as possible utility function:
as possible utility function:

Each and every individual might have its own subjective utility function, however, the probabilities are known and objective.
Recall that we have assumed ![]() , such that we restrict our considerations to functions
, such that we restrict our considerations to functions ![]() . The domain of
. The domain of ![]() can be considered as the decision maker’s accumulated wealth and the range of
can be considered as the decision maker’s accumulated wealth and the range of ![]() as the decision maker’s utility (i.e. satisfaction with respect to the cumulative wealth).
as the decision maker’s utility (i.e. satisfaction with respect to the cumulative wealth).
But what is the effect of risk on the utility function ![]() ?
?

As motivated by the St. Petersburg Paradox, there are many persons who are avers to risk-taking. Given the diversity among people there are also other types of persons. We distinguish between three types [9]:
Risk Neutral Utility
Risk-neutrality holds if every prospect is indifferent to its expected value. That is, the marginal utility is constant with increasing wealth.
Risk Averse Utility
Risk-aversion holds if every prospect is less preferred than its expected value. That is, the marginal utility of wealth.
Risk Seeking Utility
Risk-seeking holds if every prospect is indifferent to its expected value. That is, the marginal utility increases with increasing wealth.
Please note that the above descriptions are not very rigorous, however, they provide a good idea on how utility functions might be classified.
Please refer to [2] for an introduction and an overview on the mathematical treatment of decision problems with a high degree of uncertainty. In particular, so-called capacities and the Choquet integral are introduced.
Literature:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]


